© А.К.ЗвездинМагнитные молекулы и квантовая механика
А.К. Звездин
Анатолий Константинович Звездин, д. ф.-мат. н.,
рук. сект. физики магнитных явлений Института общей физики РАН.В последние два десятилетия технология активно осваивает мир нанометровых размеров. Вместо микрофизики, микроэлектроники, микротехнологии на первый план выдвинулись нанофизика, наноэлектроника, нанотехнология и т.д. В мире нанообъектов одно из центральных мест занимают ультрамалые частицы, состоящие из небольшого числа атомов (10-10000). Эти образования называют по-разному: наночастицами, нанокристаллами, квантовыми точками, но чаще всего - нанокластерами. Они привлекательны потому, что их свойства, как правило, разительно отличаются от объемных свойств материалов такого же состава. Поэтому нанокластеры рассматривают как “крупные блоки” для конструирования новых материалов и приборов.
Особенно интересны магнитные нанокластеры, так как наличие внутренней, дополнительной степени свободы - магнитного момента - придает большое разнообразие их свойствам и позволяет управлять их состоянием при помощи внешнего магнитного поля. Именно о магнитных нанокластерах и пойдет речь ниже.
Магнитная мезоскопика
Магнетизм - квантовомеханическое явление по сути. Атомы многих элементов таблицы Менделеева обладают магнитным моментом благодаря нескомпенсированному спину электронов. Среди них наибольшего внимания заслуживают атомы переходных металлов (Fe, Co, Ni и др.), лантаноидов (редкоземельных элементов) и актинидов. Молекулы, как правило, диамагнитны, хотя есть и исключения, например молекула кислорода. Что касается макроскопических веществ, то их магнитные свойства уже не так просты, поскольку не связаны напрямую с магнитными моментами составляющих их атомов или молекул.
Магнитные свойства отдельных атомов хорошо поняты. Свойства магнитных кристаллов, содержащих атомы переходных или редкоземельных элементов, также подробно изучены, хотя и в настоящее время здесь остается целый ряд вопросов. Дело в том, что возникающий в этих материалах дальний магнитный порядок не есть результат простой суперпозиции магнитных вкладов отдельных атомов. Магнитное упорядочение - это коллективный квантовомеханический эффект, в основе которого лежит специфическое взаимодействие между спинами атомов, обусловленное принципом Паули. Это взаимодействие называется обменным.
Обменное взаимодействие может индуцировать в макроскопических областях материала параллельное ориентирование спинов (ферромагнетизм), антипараллельное - в соседних узлах решетки (антиферромагнетизм) или - более сложные формы магнитного упорядочения. Магнитные кластеры представляют собой звено, соединяющее микроскопический магнетизм индивидуальных атомов и макроскопический магнетизм кристаллических и аморфных тел. Поэтому их называют иногда мезоскопическими магнитами, а новое научное направление, их изучающее, магнитной мезоскопикой. Термины “мезоскопический”, “мезоскопика” происходят от греческого слова mesos - средний, промежуточный. Мезоскопические явления очень популярны в последнее время, причем не только в магнетизме, но и во многих других областях: физике полупроводников, металлов, сверхпроводников, радиофизике, химической физике и электронике. Принципиальное значение мезоскопики состоит в том, что она дает возможность понять особенности перехода от микроскопических закономерностей к макроскопическим; эти исследования важны также для установления предельных свойств мезообъектов и, значит, определения достижимых границ миниатюризации электронных приборов и элементов памяти. И в то же время мезоскопика представляет собой богатейший источник идей для новых разработок в электронике, информационных технологиях, микромеханике и биомедицине.
При изучении свойств мезоскопических магнитов возникает ряд специфических проблем. Первая - технологическая. Как создать нанокластеры с контролируемыми размерами и свойствами? Традиционный путь, в основе которого лежит классическая в микроэлектронике технология литографии, дополняется в настоящее время новыми подходами, основанными на использовании молекулярных пучков, сканирующей туннельной микроскопии, химического синтеза, биоминерализации. Вторая проблема - как измерить физические величины, характеризующие магнитные свойства ультрамалых частиц, размер которых составляет величину порядка 1-100 нм? В идеале нужно было бы измерить характеристики индивидуальной изолированной частицы, чтобы исключить влияние взаимодействия между частицами и разброса в их размерах. Такие измерения требуют очень чувствительной техники. Среди недавних достижений в этой области нужно отметить магнитный силовой микроскоп (лучше сказать наноскоп) и интегральный СКВИД [1].
Молекулы-магниты
Намагниченность материала, состоящего из малых магнитных частиц, со временем уменьшается: exp(–t/t), где t - некоторое характерное время. Это явление называется магнитной релаксацией и обусловлено оно тепловыми флуктуациями, “помогающими” магнитному моменту частицы преодолеть энергетический барьер, который удерживает вектор момента в определенном направлении. Скорость релаксации 1/t уменьшается с понижением температуры по закону Аррениуса
t–1 = foexp(–DU/kT), (1)
где DU - величина энергетического барьера, k - постоянная Больцмана, T - температура. В данном случае DU = KV, где V - объем частицы, K - плотность энергии магнитной анизотропии, предэкспоненциальный фактор для типичных магнитных частиц fo ~ 10–9-10–10 с–1.
В последние годы было обнаружено нарушение закона Аррениуса при T ® 0. Вместо того чтобы стремиться к нулю, скорость релаксации выходит на некоторую константу. Эту особенность в поведении магнитной релаксации при очень низких температурах связывают с явлением макроскопического квантового туннелирования. Последнее означает, что при достаточно низкой температуре, когда термические флуктуации малы и не могут “перебрасывать” магнитный момент через барьер между соседними потенциальными ямами, этот вектор может переориентироваться в результате квантовой флуктуации или, другими словами, протуннелировать из одного минимума энергии (метастабильного) в другой (равновесный).
Хотя насыщение в температурной зависимости скорости магнитной релаксации при T ® 0 наблюдалось экспериментально во многих системах, у исследователей оставалось чувство неудовлетворенности, поскольку такой важный параметр как объем V туннелирующего нанокластера был плохо контролируемой величиной. А ведь зависимость скорости релаксации от объема V очень сильная (экспоненциальная), поэтому даже небольшой разброс в величине объема V приводит при низких температурах к большой неопределенности результатов. Естественным поэтому было стремление экспериментаторов найти объекты, в которых этот важный параметр - объем V - был бы строго фиксирован. И такие физические объекты были найдены [2]. Ими оказались высокоспиновые металлорганические молекулы, которые построены с участием ионов переходных элементов (Fe, Mn и др.). Подобные молекулы также часто называют магнитными кластерами. Несколько таких группирововок показаны на рис.1. Гармоничность и совершенство этих молекулярных конструкций вызывают восхищение!
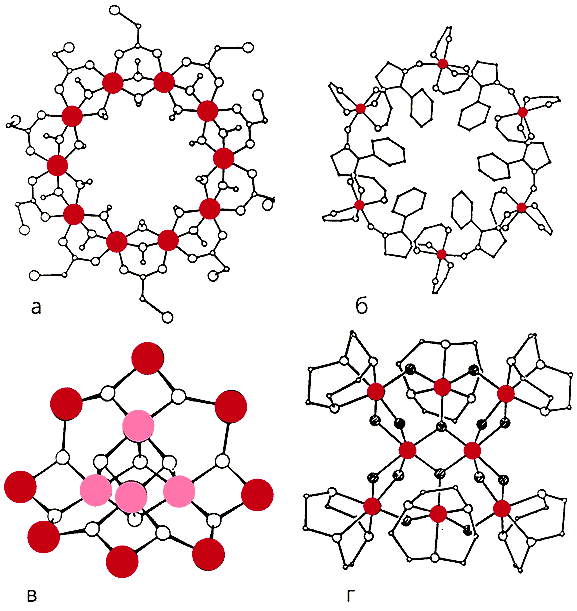
Рис. 1. Высокоспиновые молекулярные кластеры: Fe10 (а), Mn6 (б), Mn12 (в), Fe8 (г). Ионы металлов показаны цветом.
Рассмотрим, например, достаточно простой и элегантный кластер Fe10 (рис.1,а), который образно называют железным колесом. Это - десять ионов Fe3+, окруженных ионами хлора, кислорода и углерода. Взаимодействие между ионами Fe3+ носит антиферромагнитный характер, поэтому основное состояние молекулы имеет нулевой полный спин S = 0. Можно сказать, что магнитный кластер Fe10 представляет собой антиферромагнетик в масштабе одной молекулы.
Более сложно устроено марганцевое кольцо Mn6. Этот кластер представляет собой кольцевую структуру с чередующимися ионами Mn2+ и органическими радикалами, которые отмечены на рис.1,б символом R. Спины ионов Mn2+ (S = 5/2) и радикалов R (S = 1/2) связаны между собой сильным антиферромагнитным взаимодействием, поэтому кластер Mn6 оказывается ферримагнетиком, т.е. структурой с нескомпенсированным полным спином. Если все спины ионов Mn2+ направлены, скажем, вверх, а спины радикалов - вниз, то суммарный спин молекулы S = 12.
Кластер Mn12 (рис.1,в) - один из наиболее интересных для физики и приложений. Его химическая формула имеет вид
Mn12O12(CH3COO)16(H2O)4,
а устроен он следующим образом. Каждая молекула содержит группировку из 12 ионов марганца: четырех Mn4+ со спином S1 = 3/2 каждый, объединенных во внутренний тетраэдр, и восьми Mn3+ со спином S2 = 2, расположенных снаружи. Обменное взаимодействие между ионами марганца осуществляется через ионы кислорода. Конкурирующие антиферромагнитные взаимодействия приводят к образованию ферримагнитной структуры с полным спином молекулы S = 10. Упрощенно это можно представить так: у всех ионов Mn3+ спины направлены вверх, а у остальных ионов Mn4+ - вниз. В молекулярном кристалле, состоящем из рассматриваемых молекул, ацетатные группы и молекулы воды отделяют один кластер Mn12 от другого, причем настолько, что между разными кластерами остается только прямое магнитодипольное взаимодействие, величина которого чрезвычайно мала; соответствующие эффективные поля составляют величину порядка 0.01 Т. Обменные взаимодействия между магнитными моментами кластеров Mn12 еще слабее: измерения температуры Кюри по восприимчивости дают величины 50-70 мК.
Кластеры с таким большим спином редко встречаются в природе; их синтезируют в лабораториях. Мы уже отмечали в начале статьи, что они представляют большой интерес как “строительные кирпичи” для конструирования новых магнитных материалов.
Они важны также для биологии. Биологи интересуются органическими железосодержащими молекулами, обнаруженными в различных живых организмах - от некоторых бактерий, которым такие молекулы позволяют ориентироваться в магнитном поле Земли, до Homo sapiens, в мозгу которого также недавно были найдены магнитные кластеры. Пока еще никто не знает, для чего они там!
Резонансное туннелирование и квантовый гистерезис
Кластер Mn12 - хороший пример для иллюстрации квантовых свойств мезоскопических магнитов. Одна из наиболее привлекательных его особенностей - наличие сильной анизотропии типа “легкая ось”. Высота энергетического барьера, обусловленного полем анизотропии, здесь (Рис.2, слева) примерно 60 K, что соответствует полю переключения Hc ~ 50 000 Э (индукция около 5 Т). На рис.2, справа приведен спектр пропускания порошкового образца Mn12, измеренный на спектрометре “Эпсилон” (ИОФ РАН) [3], который работает в субмиллиметровом диапазоне и позволяет получить детальную информацию об уровнях энергии, представленных качественно на левом рисунке. Учитывая сведения, приведенные выше, можно заключить, что молекулярный кристалл, состоящий из кластеров Mn12, аналогичен упорядоченному массиву абсолютно идентичных, очень слабо взаимодействующих однодоменных частиц. Такая система идеально подходит для экспериментов по изучению макроскопического квантового туннелирования. Свойства, близкие к перечисленным, имеют и другие кластеры: Fe8 , Fe17 и др.
Рис. 2. Схематическое изображение уровней энергии кластера Mn12 и резонансного макроскопического квантового туннелирования намагниченности в нем (слева); спектр пропускания радиоволн в субмиллиметровом диапазоне в порошковой пластинке Mn12 толщиной d = 1.23 мм при T = 16.9 К. Параметры спин-гамильтониана Р = aSz2 + bSz4 + g(S+4 + S-4), где S - спин кластера Mn12 (S = 10) определены в нашем эксперименте (Mikhin A.A. et al, 1998) и равны: a = –0.39 см–1, b = –7.7 см–1, g = 2Ч10–5 см–1.
Измерения времени t магнитной релаксации Mn12 , проведенные при температуре около 10 K, показали, что в этом кластере оно порядка нескольких миллисекунд, и это типично для суперпарамагнитных материалов (систем из слабовзаимодействующих частиц с большими значениями спинов). Однако при понижении температуры время релаксации сильно возрастает и уже при 2 K достигает примерно двух месяцев. При T > 2 K температурная зависимость этой величины следует экспоненциальному закону (1). Вычисленная из экспериментальных данных высота энергетического барьера оказалась равной 61 K, а предэкспоненциальный множитель - 4.8Ч106 Гц. При более низкой температуре имеет место насыщение времени релаксации (рис.3). Это указывает на то, что в кластере Mn12 действительно происходит квантовое туннелирование намагниченности.
Рис. 3. Полная зависимость времени магнитной релаксации нанокластера Mn12 от обратной температуры (слева) и начальные участки кривых при различных значениях индукции магнитного поля. Установленные по этим данным параметры релаксации таковы: t0 = 10–6 с, DU = 61 K, tнас = 108 с. Указаны также соответствующие магнитному полю значения температуры кроссовера T*.Тщательное экспериментальное изучение низкотемпературных свойств кластера Mn12 подтвердило этот вывод и выявило ряд новых интересных черт. Обнаружились, в частности, дополнительные квантовые особенности. Оказалось (рис. 4), что скорость релаксации - осциллирующая функция магнитного поля [4]. Рис. 2 объясняет происхождение этого эффекта. Пусть, например, индукция магнитного поля в образце возрастает. Тогда уровни энергии в метастабильной яме (область отрицательных проекций спина на направление индукции Sz < 0) начнут сдвигаться вверх, а в стабильной яме (где Sz > 0) - вниз. При каком-то значении индукции основной уровень в метастабильной яме сравняется по энергии с первым возбужденным уровнем стабильной ямы, т.е. возникнет своеобразный резонанс. При этом квантовое туннелирование резко ускорится. Очередной “всплеск” скорости туннелирования произойдет при следующем резонансе, когда основной уровень метастабильной ямы совпадает по энергии со вторым возбужденным уровнем стабильной ямы и т.д. Именно такое поведение и реализуется в эксперименте.
Рис. 4. Зависимость времени магнитной релаксации в кластере Mn12 от индукции поля. Осциллирующий характер кривой объясняется периодическим выполнением резонансных условий для уровней энергии в метастабильной и стабильной ямах (см. рис.2, слева) по мере роста магнитной индукции. Эксперимент проводился в размагничивающем поле (отрицательные значения индукции).Параллельно с измерением времени магнитной релаксации определялась и намагниченность образца как функция индукции (петля гистерезиса). Значениям индукции поля, отвечающим резонансным условиям для уровней энергий в двух ямах соответствуют ярко выраженные “квантовые” скачки на кривой намагничивания (рис. 5). Это, наверное, первый явный пример гистерезиса в квантовой системе, где и метастабильные состояния, и выход из них определяются квантовыми закономерностями [5].
Рис. 5. Гистерезисные кривые кластера Mn12 при различных температурах. Хорошо видны “квантовые” скачки намагниченности при значениях индукции, отвечающих минимумам на кривой времени магнитной релаксации (стрелки на рис.4).Недавно было предсказано и после этого экспериментально обнаружено новое мезоскопическое квантовое явление, которое наблюдается в системах с кластерами Mn12 и другими магнитными молекулами в ультрасильных магнитных полях. Такие гигантские поля с индукцией 100-1000 Т получают методом взрывов в Российском федеральном центре “ВНИИ экспериментальной физики” (Арзамас-16). Столь сильные поля вызывают перестройку внутренней структуры кластера: исходно ферримагнитная она становится ферромагнитной с сонаправленным выстраиванием спинов всех ионов Mn. Перестройка спиновой структуры по мере роста магнитного поля носит скачкообразный характер. В целом, в этом диапазоне индукций квантовые скачки намагниченности приводят к увеличению магнитного момента нанокластера [6] от 20 до 44 mB, где mB - магнетон Бора (рис. 6).Молекулярная бистабильность и память
Рис. 6. Зависимости намагниченности (кривая 1 на верхнем рисунке) и восприимчивости (кривая 2 - теория, нижний рисунок - эксперимент) магнитного кластера Mn12 от индукции магнитного поля. Скачкообразный рост намагниченности в сверхсильных полях отвечает перестройке спиновой структуры нанокластера с переходом от ферри- к ферромагнитной. По оси абсцисс на верхнем рисунке отложены значения индукции, приведенные к характерной величине внутримолекулярного обменного поля B* @ 70 Т; в абсолютных значениях положения главных максимумов кривой 2 и экспериментальной совпадают. Замечательное свойство некоторых магнитных кластеров (Mn12, Fe8 и др.) - молекулярная бистабильность. Это означает, что магнитная молекула может находиться в двух состояниях, различающихся, скажем, ориентацией магнитного момента относительно некоторого направления. Переходы между этими состояниями могут быть индуцированы, например, магнитным полем. Другими словами, такая молекула представляет собой естественный запоминающий элемент. Для характерного расстояния между молекулами ~10 нм плотность записи информации в такой молекулярной памяти превышала бы 100 гигабит/см2. Это, конечно, впечатляет, но даже если решить проблему записи и считывания, останется еще одна трудность - конечное время хранения информации. При температуре 1.5 K время магнитной релаксации в системе с Mn12, достигая большой величины ~108с, все же оказывается недостаточным для современных компьютеров; нужны более крупные молекулы с бOльшими t. Работа в этом направлении ведется.
Весьма интересна еще одна группа магнитных молекул с несколько отличным механизмом бистабильности. В некоторой области внешних параметров эти молекулы также могут находиться в двух различных электронных состояниях. Одно из них (А) характеризуется нулевым или малым значением спина, другое (B) - высоким. Обычно одно из этих состояний - основное, другое - метастабильное. Спиновые переходы A«B возникают при совпадении энергий их уровней и могут быть индуцированы действием света или магнитного поля. Такая бистабильность реализуется, например, в магнитных полимерах, содержащих двухвалентные ионы железа [7].
Квантовые измерения, мезоскопические магниты и макроскопический реализм.
Несмотря на несомненные практические успехи квантовой механики в объяснении свойств микроскопических объектов, неуловимая тонкость перехода от микрофизики к макромиру физиков продолжает интересовать и беспокоить. С момента возникновения квантовой механики и до сих пор не утихают дискуссии, в центре внимания которых такие фундаментальные вопросы, как роль измерений в квантовой физике, парадоксы Шредингера, Эйнштейна-Розена-Подольского.
Долгие годы основными объектами этих дискуссий были мысленные эксперименты. В последнее десятилетие ХХ в. появились первые реальные экспериментальные результаты, которые с одной стороны еще больше “разогрели” дискуссии, а с другой - породили новое научное направление: квантовую информатику, которая может привести к революционным изменениям в технике передачи и обработки информации.
В основе квантовой механики лежит принцип суперпозиции состояний, который надежно апробирован в физике микромира. Например, для электрона, захваченного магнитной ловушкой, проекция спина на направление магнитного поля может иметь только одно из двух значений, Sz = +1/2 и Sz = –1/2, отвечающих ориентации магнитного момента электрона вдоль и против поля. Но в определенных условиях, например при дополнительном возбуждении электромагнитной волной, электрон может находиться в смешанном состоянии, которое представляет собой суперпозицию указанных двух состояний.
На первый взгляд кажется естественным, что квантовая механика и принцип суперпозиции применимы и к макромиру. Но уже вскоре после создания квантовой механики Э.Шредингер [8] указал на то, что экстраполяция принципа суперпозиции на макромир может привести к парадоксам. Один из них - парадокс кота Шредингера - хорошо известен [9].
Почему мы не видим квантовых эффектов, например туннелирования, на макроуровне? Почему мы не видим суперпозиции макроскопически различных состояний окружающих нас объектов? Обычный ответ на эти вопросы заключается в том, что длина волны макрообъектов слишком мала, поэтому вместо интерференции (учитывающей фазы волновых функций) в макромасштабе имеет место сложение вероятностей макроскопических состояний. Однако не все физики удовлетворены таким простым объяснением.
Более глубокий анализ проблемы привлекает идеи и представления теории квантовых измерений. Уже с начала квантовой физики стало ясно, что измерение необратимо разрушает квантовое состояние. Действие принципа неопределенности в процессе измерения разрушает когерентную интерференцию волновых функций прибора и объекта, делая последнюю неопределенной. Этот эффект называют коллапсом волновой функции. Следующий шаг вперед заключается в том, что к коллапсу волновых функций, а следовательно, и к разрушению когерентного квантового поведения приводит не только измерение, но и просто взаимодействие микрообъекта с окружением. Можно сказать, что это взаимодействие выполняет роль своеобразного сита; оно отсеивает квантовые корреляции и оставляет такие состояния, которые ближе соответствуют классическому поведению системы. Этот процесс проявляется тем сильнее, чем “более макроскопична” система. Другими словами, чем теснее микрообъект связан с классическим окружением, тем ближе его поведение к классическому [10]. Проблема в том, где находится граница между квантовым микромиром и классическим макромиром. Изучение мезоскопического мира, где встречаются квантовые и классические закономерности, поможет ответить на этот вопрос. Особенно интересны в этом отношении мезоскопические магниты, в которых естественно выделяется коллективная степень свободы, например магнитный момент, сравнительно слабо связанный с окружением и позволяющий достаточно детально проследить за его динамикой. Первые такие эксперименты уже сделаны [11].
Компьютеры и информация в квантовом мире
Рассмотренные выше квантовые свойства магнитных молекул, да и в целом - магнитная мезоскопика, представляют интерес в проблеме квантовых компьютеров [12], а также в задачах квантовой телекоммуникации и криптографии [13]. Это очень актуальные направления, и их естественно объединить единым термином “квантовая информатика” (см. статью в журнале "Вестник РАН" - V.V.).
Информация в квантовом компьютере кодируется в квантовых битах или q-битах [14]. Как и бит, q-бит реализуется в системе с двумя состояниями (условно 0 и 1), но, в отличие от первого, второй допускает суперпозицию этих состояний и, значит, более “информативен”. Физической реализацией q-бита может служить любая двухуровневая система (спин, фотон, атом, молекула, ион), волновая функция которой определяет все его значения. Сообщение представляет собой последовательность N q-битов, т.е. отвечает волновой функции N переменных. Каждому элементу алгебры логики может быть поставлен в соответствие свой гамильтониан в пространстве состояний бистабильной системы.
Вычисления отвечают законам эволюции состояний квантовой механики и, следовательно, описываются решениями уравнения Шредингера. Последнее обратимо во времени, поэтому вычисления и не сопровождаются потерей информации.
Простейший логический элемент - оператор преобразования между чистыми состояниями 0«1. Для спиновой системы этому оператору отвечает одна из матриц Паули sx. Если в качестве значений q-бита выступает проекция спина или поляризация фотона, то такая операция представляет собой поворот соответствующего вектора на угол p/2. В классической информатике этому элементу соответствует операция “не”. Уже найдены и экспериментально опробованы реализации и других логических элементов, так что на сегодня в квантовой информатике в принципе известно, как осуществить вычисления для произвольной логической функции.
Квантовый компьютер в целом представляет собой систему, состоящую из определенного набора ячеек, состояния которых кодируются q-битами, и логических элементов; состояние компьютера в любой момент времени определяется полной волновой функцией, зависящей от координат всех ячеек и их состояний. Эволюция во времени (процесс вычислений) определяется Гамильтонианом квантового компьютера.
Информация (классическая) на “входе” компьютера задает состояния всех ячеек в начальный момент времени, информация на “выходе” определяется их состояниями по окончании процесса вычислений. Главное достоинство квантового компьютера основано на использовании принципа суперпозиции, позволяющего обрабатывать информацию параллельно, что колоссально ускоряет вычисления. Например, квантовый компьютер, оперирующий с 200 q-битами, может достичь такого же эффекта при разложении 400-разрядного числа на простые множители (это важная задача криптографии), как 2200 одновременных вычислений с классическими битами. Невозможно представить себе обычный компьютер с таким количеством процессоров. Специалисты говорят по этому поводу, что квантовый компьютер может производить подобные вычисления экспоненциально быстрее, чем лучшие из известных в настоящее время классических алгоритмов.
Возникает вопрос: если квантовый компьютер столь эффективен, что мешает его созданию? Основная фундаментальная проблема здесь - потеря когерентности сложной и весьма запутанной волновой функции компьютера за счет взаимодействия с окружением. Причем, как отмечено выше, это взаимодействие разрушает в первую очередь именно квантовые корреляции, которые и составляют основу параллельной работы квантового компьютера. В настоящее время разрабатываются специальные схемы защиты квантовой информации от влияния окружения, главным образом за счет введения избыточности и на этом пути достигнуты успехи.
Другая серьезная проблема - обеспечение ввода и вывода информации и управление логическими элементами на атомном уровне. Магнитные молекулы здесь представляются особенно перспективными, поскольку они обладают большим спином в сочетании с бистабильностью, и, следовательно, достаточно сильным взаимодействием между собой и с внешними приборами. Роль бистабильной двухуровневой системы в этом случае может играть мезоскопический спин магнитной наночастицы. Благодаря сильной (экспоненциальной) зависимости частоты туннелирования от высоты потенциального барьера могут быть созданы элементы логики, управляемые изменением его высоты.
Квантовые методы обработки и передачи информации (криптография и телекоммуникация) уже выходят из лабораторий в мир практики. Насколько реальна идея квантовых вычислений, в настоящее время пока трудно однозначно оценить. Древняя мудрость гласит: если хочешь сделать миллион шагов, сделай хотя бы первый шаг. Квантовый компьютер делает первые шаги. Несомненно, что на этом пути можно ожидать появления новых принципиальных результатов.
Мы кратко рассмотрели некоторые свойства малых магнитных частиц и мезоскопических магнитов. Конечно, многие интересные вещи остались “за кадром”. Не желая ограничиться их скучным перечислением, автор предпочитает закончить статью словами французского физика де Бройля, одного из создателей квантовой механики, сказанные, правда, по другому поводу, но актуально звучащими и в данном контексте: “Мы никогда не должны забывать, что каждый успех нашего познания ставит больше проблем, чем решает, и что в этой области каждая новая открытая земля позволяет предположить существование еще неизвестных нам необъятных архипелагов”. * * *
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований.
Проект 99-02-17830.
Примечания
1 Интегральный СКВИД - высокочувствительный магнитометр, изготовленный методами интегральной технологии. Прибор преобразует магнитный поток в постоянный или переменный электрический сигнал. СКВИД - транслитерация английской аббревиатуры SQUID: Superconducting Quantum Interference Device, что означает сверхпроводящий квантовый интерференционный прибор. Чувствительность СКВИД’ов достигает величины (5-10)Ч10–15Т/Гц1/2 и ограничивается магнитными шумами в тщательно экранированных помещениях. По чувствительности эти приборы превосходят традиционные магнитометры на два-три порядка и помимо экспериментальной физики применяются, например, для детектирования магнитных полей, создаваемых биологическими объектами, в геофизике и геологии, исследовании магнитной восприимчивости материалов.
2 Gatteschi D. // Adv. Mater. 1994. V.6. №9. P.635-645; Gatteschi D., Caneschi A., Pardi L., Sessoli R. // Science. 1994. V.265. P.1054-1058.
3 Mukhin A.A., Travkin V.D., ZVEZDIN A.K. et al. // Europhys. Lett. 1998. V.44. №6. P.778-782.
4 Friedman J.R. et al. // Phys. Rev. Lett. 1996. V.76. P.3830; Thomas L., Lionti F., Ballou R. et al. // Nature. 1996. V. 383. P. 145–147.
5 См. предыдущую сноску, а также работы: Dobrovitskii V.V., ZVEZDIN A.K. // Europhys. Letters. 1997. V.38. P.377-382; Gunter L. // Ibid. V.39. P.1-6.
6 Звездин А.К., Лубашевский И.А., Левитин Р.З., Платонов В.В., Таценко О.М. // УФН. 1998. Т.168. С.1141-1146.
7 Kahn O., Jay Martinez C. // Science. 1998. V.279. P.44-48.
8 Эрвин Шредингер (1887-1961) - австрийский физик-теоретик, один из создателей квантовой механики. Исходя из идей французского физика де Бройля и принципа Гамильтона, разработал в 1926 г. волновую теорию движения микрочастиц. Основа этой теории - уравнение Шредингера, играющее в квантовой механике такую же роль, как уравнения Ньютона в механике классической. Лауреат Нобелевской премии (1933).
9 Этот парадокс - результат мысленного эксперимента Э. Шредингера с котом. Сам эксперимент и парадокс подробно проанализированы в обзоре: Кадомцев Б.Б. // Динамика и информация. М., 1997.
10 В некоторых работах делаются попытки внести необратимость непосредственно в квантовую теорию с целью феноменологически описать взаимодействие квантового объекта с внешним окружением, которое постоянно стремится разрушить квантовое поведение микрообъекта (см. обзор Кадомцева).
11 Awschalom D.D., Vincenzo D.P. di // Phys. Today. 1995. V.48. №4. P.43-48.
12 Vincenzo D.P. di // Science. 1995. V.270. P.255-261.
13 Tittel W., Ribordy G., Gisin N. // Physics World. 1998. March. P.41-45.
14 Слово “qubit” ввел в употребление Бен Шумахер из Кеньон-колледжа (США) в 1995 г. В отсутствие русскоязычного эквивалента автор с согласия редакции считает оправданным написание “q-бит”, произносимое “кьюбит”, как и на языке оригинала.
Декабрь 2000 |