VIVOS VOCO: К.А. Валиев, "КВАНТОВАЯ ИНФОРМАТИКА: КОМПЬЮТЕРЫ, СВЯЗЬ И КРИПТОГРАФИЯ"

Информатика - наука о методах обработки информации - стала быстроразвивающейся областью человеческой деятельности. Понятие информации тесно связано с физическим понятием энтропии. Она не существует вне физики, то есть реального мира. В информационных системах ее носители - физические тела, с состояниями которых связываются информационные понятия и символы, а с эволюцией состояний физических тел связываются процессы обработки информации.

Эти общие положения обретают наглядность при физическом отображении цифровых информационных систем, построенных на двоичной системе исчисления. Их отображением могут служить любые физические системы, имеющие два устойчивых состояния и способные совершать переходы между ними под воздействием внешних сигналов (механические или электрические переключатели (ключи)) (табл. 1).

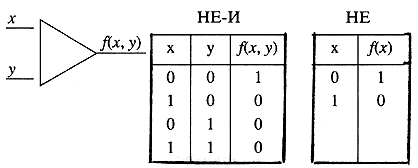
При анализе информационных систем полезно выделить минимальной сложности операции (булевы функции), из которых могут быть построены системы любой сложности. Доказано, что классические двоичные системы могут быть построены из единственного элемента НЕ-И, имеющего два входа х, у (0; 1) и один выход f(x,у), значение f(x,у) = 1, когда х = у = 0, и f(x,у) = 0 во всех других случаях:

Одновходовой элемент НЕ в современных микропроцессорах строится на двух полевых транзисторах (рис. 1). Передаточная характеристика элемента (рис. 2) соответствует булевой функции НЕ: когда на входном электроде низкое напряжение (лог. |0>), на выходном электроде высокое напряжение (лог. |1>), и наоборот.

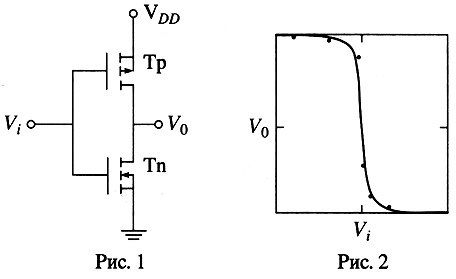Рис. 1. Принципиальная схема логического элемента НЕ на полевых транзисторах. Напряжение питания V_DD приложено к последовательно соединенным р-канальному (открыт, когда V_i< 0) и n-канальному (открыт, когда V_i> 0) транзисторам

Рис. 2. Нелинейная зависимость выходного напряжения V₀ рот входного Vi описывает логическую операцию НЕ, если низкое напряжение считать логическим |0>, и наоборот

Элементы современных систем обработки информации - электронные лампы, транзисторы, диоды, фотоприемники, светодиоды и лазеры - являются "классическими" приборами. Определение "классический" отражает то обстоятельство, что внешние, функциональные свойства приборов (например, токи и напряжения на электродах) описываются законами классической физики. Конечно, внутренние процессы в приборах, происходящие на атомном уровне, являются квантовыми. Таковы зоны энергии и рассеяние электронов в полупроводниковой структуре транзисторов, процесса туннелирования в туннельно-резонансных диодах, излучение и поглощение фотонов в активной среде лазеров. Эти внутренние процессы описысываются квантово-статистическим методом.

Главной тенденцией развития технологии твердотельных приборов микроэлектроники стало непрерывное уменьшение размеров элементов приборов. Сейчас минимальные размеры близки к 0.1 мкм - это 500 атомных размеров. Размеры меньше 0.1 мкм называются нанометровыми (1 нм = 0.001 мкм), а приборы - наноэлектронными.

Экстраполяция тенденции уменьшения размеров элементов приборов показывает, что атомные размеры в твердотельной технологии будут достигнуты через 20-30 лет. Не переоценивая точности этого предсказания, можно быть уверенным, что уровень технологии атомных размеров будет достигнут, и такая технология позволит изготавливать микросхемы, работающие на квантовых принципах. Другие технологии на атомном уровне (например, технологии на ионах и атомах в ловушке) также могут использоваться для построения квантовой элементной базы информационных систем.

КВАНТОВАЯ ФИЗИКА И КВАНТОВАЯ ИНФОРМАТИКА

На рубеже Х1Х-ХХ вв. возникла великая физическая теория, описывающая свойства частиц и их движение в микромире - квантовая физика (механика). Одним из поводов к этому послужила невозможность с точки зрения классической физики описать спектр излучения абсолютно черного тела в коротковолновой части, так называемая "ультрафиолетовая катастрофа". В течение четверти века усилиями Планка, Н. Бора, Э. Шредингера, В. Гейзенберга был создан математический аппарат квантовой механики и решены основные задачи о квантовом описании движения объектов микромира: электронов, атомов и молекул; электронов и атомов в твердых телах; взаимодействия излучения и атомов (атомная спектроскопия).

На квантовом уровне мир описывается уравнением Шредингера:

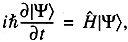
Оператор Н линейный:

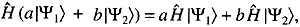
следствием чего является квантовый принцип суперпозиции состояний. Если квантовая система может существовать в состояниях |Y₁> и b|Y₂>, то она может столь же "законно" существовать и в состояниях их суперпозиции: a|Y₁> + b|Y₂> = |Y>, a, b - комплексные амплитуды, |a|² + |b|² = 1.

Эволюция состояний квантовых систем происходит согласно квантовому уравнению Шредингера. Свяжем с состояниями квантовой системы (частицы) информационные понятия и символы. Установление такого соответствия превращает квантовые системы в квантовые приборы. Последние можно рассматривать как квантовую элементную базу информационных систем. Эволюция состояний квантовых приборов представляет информационный процесс.

Таким образом, подчинение прибора уравнению Шредингера (и принципу суперпозиции) выделяет его в класс квантовых приборов. Управление прибором извне (внешним полем) происходит также согласно уравнению Шредингера. Очевидно выделенными оказываются квантовые частицы (системы) с двумя состояниями, на которые отображаются информационные системы, построенные на двоичной системе исчисления.

КУБИТЫ - КВАНТОВЫЕ БИТЫ И ОПЕРАЦИИ НАД НИМИ

Квантовая система с двумя различимыми состояниями |Y₀>, |Y₁> способная нести 1 бит информации, получила название кубит (qubit) [1]. Если состояния |Y₀>, |Y₁> связаны с двумя уровнями энергии E₀ < Е₁, то можно говорить о двухуровневой системе. Простейшим случаем двухуровневой квантовой системы является спин ядра атома или электрона / = 1/2 в постоянном внешнем поле B₀: два уровня энергии и состояния соответствуют проекциям спина на направление B₀ (рис. 3).

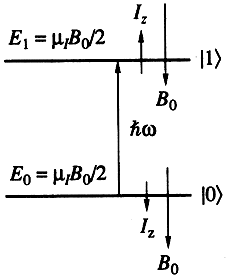Рис. 3. Состояния спина I_z = ±1/2 - и его уровни энергии E_0,1 = ±m_iB₀/2
во внешнем поле B₀ представляют логические состояния кубита |0> и |1>

Два оптических уровня энергии и состояния электрона в ионе также могут быть выбраны в качестве двух состояний кубита (рис. 4).

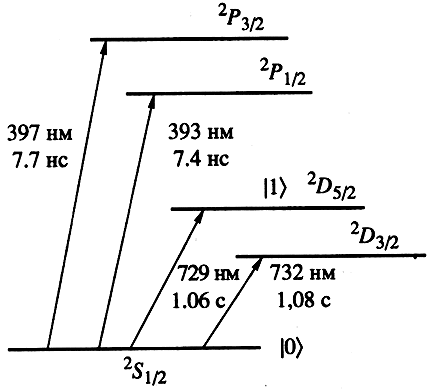Рис. 4. Состояния иона Са⁺, соответствующие уровням энергии ²S_1/2 (основной) и ²D_5/2 (метастабильный) выбраны за логические |0> и |1>. Числа у стрелок показывают длину волны лазера, вызывающего переход, и время жизни иона на соответствующем уровне

В других случаях состояния |Y₀>, |Y₁> могут различаться поляризацией (фотона) или фазой (сверхпроводника). Квантовая система может быть макроскопической (сверхпроводники, сверхтекучие жидкости, бозе-газ), отдельной атомной частицей, или колебательной модой. Все эти системы могут быть использованы в качестве кубита.

Некоторое число п кубитов образуют квантовый регистр компьютера. В ходе выполнения квантового алгоритма состояния кубитов изменяются согласно плану выполнения алгоритма. Доказано, что любой квантовый алгоритм может быть разложен на последовательность преобразований состояний отдельных кубитов и пар кубитов (одно- и двухкубитовые преобразования, или "вентили"). Чтобы построить квантовый компьютер, необходимо уметь осуществлять:

1) любые суперпозиции состояний |0> и |1> любого кубита,

2) контролируемый одним ("контролирующим") кубитом преобразование НЕ другого ("контролируемого") кубита.

Взглянем на таблицу 2.

Контролируемое преобразование можно осуществить только при наличии физического взаимодействия между контролирующим и контролируемым кубитами. Чтобы выполнить необходимые операции на кубитах, на них воздействуют импульсами внешнего резонансного поля. Квантовая эволюция состояния кубита |Y_(t)> совершается согласно уравнению Шредингера, где H_i (t) = -me₀cos(wt + j) - энергия взаимодействия дипольного момента m кубита и внешнего резонансного поля (например, лазера). При этом необходимо иметь возможность воздействовать избирательно на любой избранный кубит.

СХЕМА КВАНТОВОГО КОМПЬЮТЕРА

Мысль о возможности построения квантового компьютера впервые высказал Р.П. Фейнман [2]. Схематически структура квантового компьютера представлена на рис. 5. Квантовую часть компьютера составляют п кубитов. К каждому из них может быть приложено селективное воздействие импульсами резонансного внешнего переменного поля. Включение генераторов полей и адресация их излучения на данный кубит осуществляется под управлением классического компьютера. Эволюция состояния кубитов изображается вдоль горизонтальных линий (ось времени) в виде последовательности однокубитовых и двухкубитовых вентилей. До того как "запустить" вычислительный процесс на квантовом компьютере, все n кубитов должны быть приведены в состояние |0>. Эта процедура носит название "инициализация". Это вовсе не тривиальная операция. Если в качестве кубитов используются ядерные спины, для инициализации потребуется охлаждение до температур порядка I mK или поляризация спинов накачкой. Ввод данных и исполнение алгоритма совершаются применением однокубитовых и двухкубитовых вентилей. По завершении алгоритма результат вычисления будет записан в конечном квантовом состоянии кубитов. Чтобы "считать" результат, необходимо провести квантовое измерение состояния кубитов (одного или нескольких). Квантовые алгоритмы решения сложных задач могут состоять из большого числа (~10⁹) операций (вентилей), выполняемых на компьютерах, содержащих -10³ кубитов.

Сейчас разработано немного алгоритмов для квантовых компьютеров, но в том, что сделано, получены ошеломляющие результаты. В 1994 г. Шор создал алгоритм факторизации - то есть определения простых множителей больших п разрядных чисел [3]. На классическом компьютере для этого требуется экспоненциально большое число операций. Недоступность этой задачи современным компьютерам используется для кодирования (шифрования) секретной информации (в RSA криптосистемах). Шор показал, что квантовый компьютер способен решить эту задачу за n³операций. Коэффициент ускорения задачи при больших п может быть очень большим. Такое же ускорение имеет место при решении на квантовом компьютере задач квантовой физики [4]. В то же время установлено, что многие алгоритмы, выполняемые неплохо на классических компьютерах, не ускоряются на квантовом [5].

Ускорение процесса решения задач на квантовом компьютере лежит в квантовой природе кубитов. Квантовость кубитов приводит к нескольким феноменам.

1. Гильбертово пространство состояний квантовой системы из n кубитов имеет огромную размерность, равную 2ⁿ. Физически это означает, что система имеет 2ⁿ базовых состояний, а состояние компьютера описывается суперпозицией из этих 2ⁿ базовых состояний. При воздействии на какой-либо кубит одновременно изменяются все 2ⁿ базовых состояний. Этот феномен носит название квантового параллелизма.
2. Вычислительный процесс носит характер интерференции, так как амплитуды базисных состояний являются комплексными числами. Квантовый компьютер можно рассматривать как сложное интерференционное устройство, в котором интерференция состояний создает вычислительную мощь компьютера.

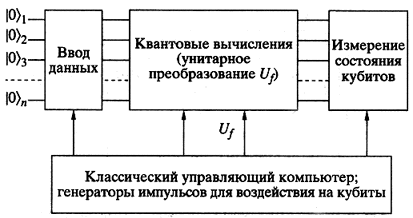
Рис. 5. Квантовый компьютер состоит из n кубитов и позволяет проводить одно- и двухкубитовые операции над любым из них (или любой парой). Эти операции выполняются под воздействием импульсов внешнего поля, управляемого классическим компьютером

С возникновения идеи создания квантовых компьютеров математики нашли новую важную задачу: разработать квантовые алгоритмы решения вычислительных задач математики и определить, где есть ускорение и каково оно. В алгоритме Шора, по-видимому, впервые обнаружен феномен, когда класс сложности задачи коренным образом изменяется в зависимости от того, на каких физических принципах строится вычислительный процесс. При выполнении задачи на любом из классических компьютеров принадлежность задачи к классу будет неизменной.

По-видимому, место квантовых компьютеров в компьютерном мире XXI в. можно определить следующим образом: они не вытесняют, а дополняют существующий компьютерный мир. Их надо будет применять в тех случаях, когда они дают большое ускорение решения задачи.

ВОЗМОЖНЫЕ ПУТИ СОЗДАНИЯ КВАНТОВЫХ КОМПЬЮТЕРОВ

К настоящему времени предложены различные пути реализации квантовых компьютеров [6-15]. Наиболее впечатляющие результаты получены в экспериментах по квантовым вычислениям методом импульсного ядерного магнитного резонанса в молекулярных жидкостях (ансамблевый квантовый компьютер) [6, 7]. Другие авторы предлагают использовать в качестве элементной базы квантовых компьютеров ионы в ловушках в вакууме [8], ядерные спины атомов ³¹Р в монокристаллическом кремнии [9], спины одиночных электронов в квантовых точках в двумерном газе в полупроводниковых гетероструктурах [10], атомы в резонаторах электромагнитного поля [11]. Возможно создание кубитов на состояниях сверхпроводников, разделенных переходами Джозефсона и различающихся числом зарядов [12, 13] или фазой сверхпроводников [14]. Интересно, что модели квантовых компьютеров могут быть построены на линейных оптических элементах (делители пучка, поляризаторы, фазовращатели, интерферометры) [15].

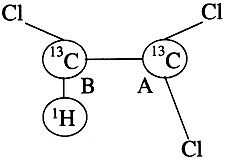
В ансамблевом ядерном магнитнорезонансном квантовом компьютере кубитами выступают спины - ядер водорода (протоны) и углерода ¹³С в молекулах жидкости. Так, в молекуле трихлорэтилена спины ядер двух атомов ¹³С и одного протона образуют три кубита. Два атома ¹³С химически неэквивалентны и поэтому имеют различные частоты ядерного магнитного резонанса w_A и w_B в заданном внешнем постоянном магнитном поле B₀, протон будет иметь третью резонансную частоту w_C. Подавая импульсы внешнего переменного магнитного поля на частотах (ид, tog, о)с, мы селективно управляем квантовой эволюцией любого из этих спинов (выполняем одноку битовые вентили). Между спинами ядер, разделенных одной химической связью ¹H-¹³С и ¹³С-¹³С, имеется магнитное контактное взаимодействие, что позволяет построить двухкубитовые вентили.

Макроскопически большое число (~10²⁰) молекул в пробирке импульсного ЯМР спектрометра, запрограммированного на выполнение квантового алгоритма на трехкубитовом компьютере /_А, /_B, /_C представляет собой ансамбль работающих параллельно квантовых компьютеров. "Ансамблевость" компьютера в данной ситуации позволяет решить трудные проблемы инициализации компьютера (т.е. приведения всех кубитов в состояние (0) перед вычислением) и измерения состояния кубитов по завершении процесса вычислений. Состояния |0> и |1> некоторого кубита в конечном состоянии определяется путем наблюдения знака (фазы) линии резонансного поглощения: в случае |0> наблюдается, например, линия поглощения, а при |1> - излучения.

К настоящему времени на спиновых двух- и трехкубитовых квантовых компьютерах выполнен модельный квантовый алгоритм Дойча-Иозса по определению типа дискретной функции от дискретного аргумента [16], алгоритма Гровера поиска в базе данных [17], алгоритм с квантовой коррекцией ошибок [18].

Эти результаты произвели большое впечатление на научное сообщество. Однако анализ показывает, что масштабирование квантового компьютера на спинах в молекулах на число кубитов порядка 10³ вряд ли возможно: трудно представить, что такое количество спинов ядер будут иметь различимые частоты резонанса.

Интересна идея создания квантового компьютера на ловушках в вакууме. "Подвешенные" в вакууме ионы (атомы) напрямую осуществляют идею максимально изолированных от окружающего мира квантовых частиц. Связь ионов с окружающим миром сохранена только для удержания ионов в ловушке (электроды с напряжениями) и управления квантовой эволюцией (сфокусированные лазерные пучки). Эксперименты в этом варианте квантового компьютера ведутся в Лос-Аламосе и Национальном институте стандартов США [19,20].

Большой интерес вызывают предложения по созданию элементов квантовых компьютеров на твердом теле, так как в этом случае можно использовать накопленный опыт микроэлектронной технологии, а сами квантовые компьютеры могли бы иметь сходство с "чипами" микросхем. В [9] предложено использовать в качестве кубитов спины / = 1/2 ядер атомов фосфора ³¹Р в монокристаллическом кремнии (рис. 6). Частотой магнитного резонанса на ядрах ³¹Р в кремнии можно управлять, подавая на наноэлектрод над атомом электрическое напряжение V: оно поляризует электронную оболочку атома и изменяет константу А так называемого сверхтонкого взаимодействия электронного S и ядерного / спинов атома: H_i= A(V) • S. Таким образом достигается селективный доступ внешнего резонансного магнитного поля к спину ядра данного атома. Структура с единичным атомом, встроенным в заданную точку под электродом, отдаленно напоминает структуру полевого транзистора. Затвор последнего управляет движением электронов проводимости от истока к стоку. В случае кубита напряжения на затворе управляют движением электрона внутри атома, поляризуют атом и изменяют резонансную частоту кубита, связанного со спином его ядра.

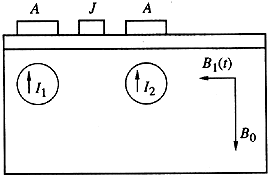
Рис. 6. Разрез структуры кремниевого квантового чина. Под наноэлектродами А в безспиновом кремнии находятся одиночные неионизованные атомы ³¹Р. Ядерные спины I₁, I₂ выступают в качестве кубитов. Напряжения на электродах А управляют частотой магнитного резонанса ядерных спинов; с помощью напряжения на электроде J "включается" взаимодействие спинов, необходимое для выполнения операции Контролируемое НЕ

Интересны предложения о создании элементов квантовых компьютеров на- сверхпроводниках [12-14]. Одним из достоинств этих предложений является возможность использования структур с наноразмерами (структуры с Джозефсоновскими контактами), технология которых в значительной мере разработана.

Три сегодняшних технологии могут оказаться полезными при построении квантовых компьютеров на твердом теле: молекулярная эпитаксия, нанолитография, зондовая микроскопия. Молекулярная эпитаксия позволяет создавать совершенные моноатомные слои кристаллов, то есть атомный размер достигается по толщине. Методы зондовой микроскопии позволяют, во-первых, наблюдать поверхность тел с атомным разрешением. Во-вторых, зонды можно использовать как технологическое средство типа атомного манипулятора: перемещать, доставлять, снимать атомы с поверхности. Зонды могут работать и как катализаторы локальных поверхностных химических реакций (окисление, травление, осаждение материала), доставляя энергию локального возбуждения (химической активации) в форме электрического тока, напряжения, фотонов, механической энергии (деформации). Наконец, зондовые методы могут сыграть роль приборов для измерения состояний атомных частиц. Методы электроннолучевой нанолитографии с разрешением 1-10 нм также могут занять существенное место в технологии атомных структур квантовых компьютеров.

Другим направлением атомной технологии является вакуумная технология ионов и атомов в ловушках. Эта технология предусматривает размещение ионов или атомов в области минимума потенциала, создаваемого системой электродов и электромагнитных полей. Для охлаждения (замораживания) теплового движения атомов используется технология лазерного охлаждения. Первоначально технология "ионы в ловушках" развивалась в целях создания квантовых стандартов частоты; в настоящее время большой интерес к этой технологии связан с задачей создания квантовых компьютеров [19,20].

Технологии с атомным разрешением имеют довольно высокий уровень зрелости и работа с отдельными атомами является экспериментальной реальностью. Тем не менее предстоит пройти большой путь, пока будет построен полномасштабный (10³-10⁴ кубитов) квантовый компьютер. Пока неясно, какой способ построения квантового компьютера окажется предпочтительным. Настоящий этап исследований характеризуется поиском возможностей их построения по всему фронту физики. То и дело возникают новые идеи, новые предложения. Оптимисты полагают, что среди новых идей могут найтись "прорывные", которые приблизят день построения полномасштабного квантового компьютера. По-видимому, одной из таких идей можно считать идею применения метода квантовой коррекции ошибок.

КВАНТОВАЯ КОРРЕКЦИЯ ОШИБОК В КВАНТОВОМ КОМПЬЮТЕРЕ

В самом начале развития идей о квантовом компьютере физики обнаружили и грозного противника этой машины. Имя этого противника -декогерентизация. Кубиты компьютера нельзя полностью изолировать от внешнего мира: кубиты работают в условиях шумового воздействия внешней среды. Флуктуации напряжений на электродах, шумовые токи, неточности выполнения самих импульсных воздействий на кубиты в ходе вычислительного процесса - все это вносит неконтролируемые ошибки в фазы и амплитуды состояний кубитов в ходе вычислительного процесса. По истечении времени, равном времени деко-герентизации квантовых состояний системы кубитов, контролируемый вычислительный процесс прекратится, эволюция квантового компьютера приобретет случайный (диффузионный) характер. Время декогерентизации, как правило, будет меньше времени, необходимого для выполнения сложного алгоритма, состоящего из большого числа (-10⁹) вентилей.

Выход из этой, казавшейся тупиковой, ситуации был найден в применении методов квантовой коррекции ошибок [21]. Методы коррекции ошибок хорошо известны из теории обычных (классических) компьютеров. Смысл их в том, что логические |0> и |1> кодируются большим числом битов; анализ кодовых комбинаций позволяет найти и удалить ошибку. Эти методы удалось разработать в квантовом варианте, где ошибки могут быть фазовыми и амплитудными. Выяснилось, что если вероятность ошибки при выполнении одной элементарной операции ниже некоторого порогового уровня, вычислительный процесс можно длить сколь угодно долго. Это означает, что операции квантовой коррекции ошибок удаляют из компьютера больше ошибок, чем вносят. Этот вывод очень важен: по существу, он имеет силу теоремы существования полномасштабного квантового компьютера.

КВАНТОВАЯ СВЯЗЬ И КРИПТОГРАФИЯ

Из обширной области разработки квантовых методов связи и криптографии мы коснемся последствий создания квантовых компьютеров и систем связи для двух современных наиболее популярных криптосистем: для системы с открытым ключом (RSA система, Rivest, Sharnir, Adieman, 1977) и системы с ключом одноразового пользования (Vernam, 1935).

Сразу отметим, что в основе системы RSA лежит предположение о том, что решение математической задачи о разложении больших чисел на простые множители на классических компьютерах невозможно; оно требует экспоненциально большого числа операций и астрономического времени.

Квантовый алгоритм Шора дает возможность вычислить простые множители больших чисел за практически приемлемое время и взломать шифры RSA криптосистем. Таким образом, для RSA криптосистем квантовый компьютер - плохая новость.

Для криптосистем с ключом одноразового пользования квантовые методы связи оказываются хорошей новостью: они позволяют обнаружить наличие подслушивания при передаче ключа. Эта возможность основана на квантовом принципе неопределенности Гейзенберга, который гласит, что измерение изменяет состояние измеряемой квантовой системы. Пусть ключ передается по световолокну с помощью фотонов, и информация закодирована в поляризации фотонов [22]. Тогда подслушивание заключается в перехвате и измерении поляризации пересылаемых фотонов; после измерения они пересылаются адресату. При наличии подслушивания адресат обнаружит, что 25% фотонов приходят к нему с "неправильной" поляризацией. Если этих ошибок нет, то передача ключа не подслушивается, и им можно пользоваться. Таким образом, квантовые методы обеспечивают гарантированную секретность ключа одноразового пользования. Эксперименты по передаче ключа выполнены на расстояния до 40 км.

Квантовые каналы связи дают и другие возможности.

1. С помощью одного кубита можно передавать 2 бита информации ("плотное квантовое кодирование").

2. Возможна передача неизвестного квантового состояния ("квантовая телепортация") по классическому каналу, если абоненты связи предварительно поделили коррелированную пару квантовых частиц. Потенциальные возможности применения этих феноменов еще не выяснены.

* * *

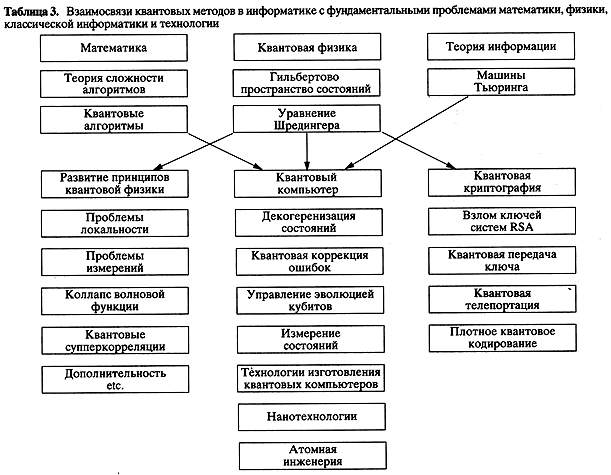
Идеи квантового компьютера и квантовой связи (криптография) возникли через сто лет после рождения идей квантовой физики. Возможность построения квантовых компьютеров и систем связи подтверждается современными теоретическими и экспериментальными исследованиями. Новая техника XXI в. рождается путем синтеза новых идей в математике, физике, информатике, технологии. Взаимодействие фундаментальных отраслей науки и технологии, рождающее новую технику, показано в таблице 3. Важно подчеркнуть, что в процессе решения задач квантовой информатики происходит развитие и углубление понимания основ квантовой физики, подвергаются новому анализу и экспериментальной проверке основные ее проблемы - локальности (причинности), скрытых параметров, реальности, неопределенности, дополнительности, измерений, коллапса волновой функции.

Квантовые компьютеры, если их удастся построить, будут техникой XXI в. Для их изготовления потребуется развитие технологий на наноме-тровом и атомном уровне размеров. Эта работа может потребовать значительного времени. Построение квантовых компьютеров было бы еще одним подтверждением принципа неисчерпаемости природы: природа имеет средства для осуществления любой корректно сформулированной задачи.

ЛИТЕРАТУРА

1. Shumacher B.W. Quantum coding // Phys. Rev. 1995. P. 2738-2747.
2. Feinman R.P. Quantum Mechanical Computer // Foundations of Physics, 1986. № 16(6). P. 507-531.
3. Shor P.W. Algorithms for quantum computation: Discrete logarithms and factoring // Proc. 35th Annual Symposium on Foundations of Computer Science (IEEE Press), 1994. P. 124-134.
4. Zalka С. Simulating quantum systems on a quantum computer//Proc. Roy. Soc. London. 1998. P. 313-322.
5. Ozhigov Y. Quantum Computer Can Not Speed Up Iterated Applications of a Black Box // quant/ph/9712051, 1997.
6. Cory D.G., Fahmy A.F., Havel T.F. Nuclear Magnetic Resonance spectroscopy: an experimentally accessible paradigm for quantum computing // Proc. of the 4th Workshop on Physics and Computation (Complex Systems Institute, Boston, New England), 1996.
7. Gershenfeld N.A., Chuang I.L. Bulk spin resonance quantum computation // Science, 1997. V. 275. P. 350-356.
8. Cirac J.I., Zoller P. Quantum Computations with Cold Trapped Ions // Phys. Rev. Lett. 1995. №20. P. 4091 ^094.
9. Каnе В.Е. A silicon based nuclear spin quantum computer // Nature. № 395. 1998. 14 May.
10. Loss D., Vincenzo D.P. Quatum Computation with Quantum Dots // Phys. Rev. 1998. № 1. P. 120-126.
11. Cirac J.I. et al. Quantum state transfer and entanglement distribution among distant nodes of a quantum network // Phys. Rev. Lett. 1997. V. 78. P. 3221.
12. Shnirman A., Schon G., Herman Z. Quantum Manipulations of Small Josephson Junctions // Phys. Rev. Lett., 1997. V. 79. P. 2371-2374.
13. Averin D.V. Adiabatic Quantum Computation with Cooper pairs // Solid State Commun. 1998. № 105. P. 659-664.
14. loffe L.B. et al. Quest SDS Josephson Junctions for Quantum Computing / cond-mat/9809116, v. 2, Jan. 1999.
15. Adami С.. Cerf N.J. Quantum Computation with Linear Optics // quant-ph/9806048, 14 June 1998.
16. Chuang I.L. et al. Experimental realization of a Quantum algorithm / /Nature, 1998. V. 393. P. 143-146.
17. Jones J.A., Mosca M., Haasen R.S. Implementation of a Quantum search algorithm on a quantum computer // Nature, 1998. V. 393. P. 344-346.
18. Cory D.G. et al. Experimental Quantum Error Correction // quant-ph/9802018 6 Feb. 1998.
19. Hughes R.J. et al. The Los Alamos Trapped Ion Quantum Computer Experiment // Fortschr. Phys. 1998. № 4-5. P. 329-361.
20. Wineland D.J. et al. Experimental issues in coherent quantum-state manipulation of trapped ions // J. Res. Natl. Inst. Stand. Tech. 1998, № 103. P. 259.
21. Steane A. Multiple particle interference and quantum error correction // Proc. Roy. Soc. London, 1996. P. 2551-2577.

22. Titlel W., Rihordy G., Gisin N. Quantum cryptography // Physics World. 1998. March. P. 41-45.