VIVOS VOCO: Б.А. Прудковский, "О консервной банке, пружине и прокатном стане"

Будем считать, что вам не раз приходилось вскрывать консервные банки. И время от времени вы задавались вопросом: неужели металлический лист, из которого сделана банка, нельзя изготовить потоньше? Тогда, например, из материала для одной консервной банки можно было бы сделать две или даже три. В чем же дело? Почему металлурги не экономят металл? Давайте попробуем разобраться.

Консервные банки делают из стального тонкого листа - жести. Жесть получают холодной прокаткой. Нужно сказать, что с наиболее раннего достоверного упоминания о применении прокатки для деформирования металла прошло более 500 лет. В 1486 году великий художник, архитектор, ученый и инженер Леонардо да Винчи изобразил прокатный стан для получения тонкой ленты из золота и серебра, идущей на украшения. Такой стан имел два гладких валка диаметром около 40 мм, которые вращали вручную. Сущность процесса прокатки с тех пор принципиально не изменилась (рисунок 1, а). В зазор между вращающимися в разные стороны валками затягивается металлическая полоса, толщина которой (h_о) больше величины этого зазора (S_о). Полоса под действием валков испытывает пластическую деформацию изменения формы и должна выходить из валков с толщиной, равной, казалось бы, величине зазора между ними (увеличиваясь при этом в длине и оставаясь той же ширины В). Однако фактически толщина прокатанной полосы (h₁) бывает всегда больше зазора между валками. Почему?

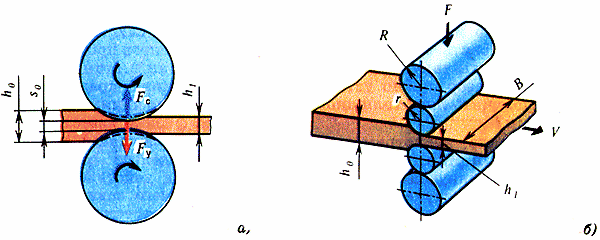
Рис. 1

Деформация полосы происходит в результате действия сил, приложенных к ней со стороны валков. Каждый валок действует на полосу, и согласно третьему закону Ньютона полоса действует на валок с такой же по величине силой; ее называют силой сопротивления деформированию или просто сопротивлением деформированию. Под действием этой силы происходит упругая деформация валков и других деталей прокатного стана, Первоначально установленный зазор между валками увеличивается, и на столько же увеличивается толщина прокатанной полосы. Другими словами, мы всегда получаем толщину полосы несколько большую, чем зазор (S_о) между валками. Для уменьшения деформации рабочих валков применяют опорные валки (рисунок 1,б).

Ну хорошо, скажете вы, тогда надо сделать зазор между валками меньше требуемой толщины жести и получить нужную толщину. Логично! Хотя это лишь один из способов.

Но так ли все просто? Толщина жести "нормальной" консервной банки равна 0,2-0,25 мм. Какой же зазор нужно установить между валками, чтобы получить такую толщину листа? А какой зазор нужно установить, чтобы получить лист толщиной, скажем, 0,1 мм?

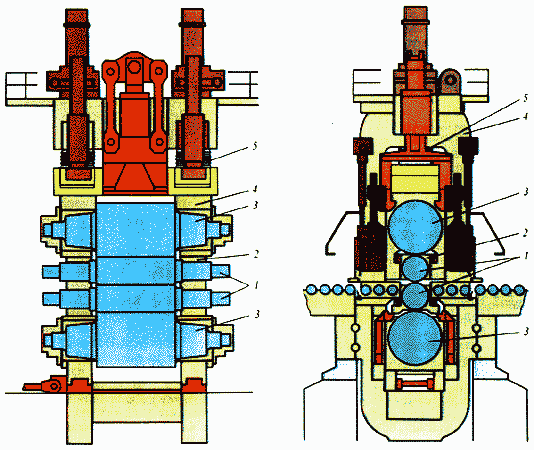
Рис. 2

Давайте сначала посмотрим, как устроен прокатный стан (рисунок 2). Валки (1), деформирующие полосу, не могут висеть в воздухе. Они крепятся на подшипниках (2) вместе с опорными валками (3) в раме, называемой станиной прокатного стана (4), Требуемый зазор между валками при прокатке устанавливается с помощью винтов, которые называют нажимными винтами (5).

Сила сопротивления деформированию, действующая на рабочие валки со стороны прокатываемой полосы, вызывает упругую деформацию не только этих валков, но и опорных, а также нажимных винтов, станины и других элементов прокатного стана. Прокатный стан в этом случае ведет себя как пружина, правда, не совсем обычной конструкции.

Из курса физики известно, что всякая пружина обладает жесткостью, которая определяет ее степень деформации под действием приложенных сил. От чего зависит жесткость прокатного стана, если его рассматривать как пружину? Упрощенно можно сказать, что (как и жесткость пружины) она зависит от его конструкции. Например, стан с двумя валками обладает значительно меньшей жесткостью по сравнению со станом, имеющим четыре валка, два из которых являются опорными. Есть и более жесткие станы, с бблыпим числом опорных валков.

Теперь ясно: чтобы определить величину зазора, необходимого для получения жести заданной толщины, нужно знать величину жесткости прокатного стана. Как же ее найти? Есть, конечно, расчетные методы, но для уже существующего стана ее проще измерить.

Установим нажимными винтами какой-либо зазор S_о между рабочими валками. Теперь с помощью распорного устройства будем каждый раз увеличивать этот зазор на величину DS и измерять динамометром силу упругости стана. На рисунке 3 результаты нескольких таких измерений представлены в виде графика зависимости силы упругости F_y от величины зазора между рабочими валками. Эта зависимость изображается прямой линией, так как деформации деталей прокатного стана упругие и справедлив закон Гука.


*Рис. 3*	*Рис. 4*

Тангенс угла a характеризует жесткость стана. Чем больше tg a, тем больше жесткость. Конечно, в идеале угол a должен был бы стремиться к p/2, но... все тела деформируются. Теперь посмотрим, что происходит в реальном процессе прокатки. Мы уже говорили, что согласно третьему закону Ньютона валки действуют на прокатываемую полосу с такой же по величине силой, с какой полоса действует на валки. Эту силу мы назвали сопротивлением деформированию. Но как найти ее величину? Очевидно, что для прокатного стана, обладающего определенной жесткостью, его упругая деформация будет зависеть от сопротивления деформированию прокатываемой полосы. Если на одном и том же стане прокатывать полосы из алюминия, меди и стали, то упругая деформация стана в каждом конкретном случае будет разной. При прокатке алюминия она будет меньше, при прокатке меди - больше, а при прокатке стали - еще больше. Почему?

Вспомним диаграмму растяжения металлов. Для алюминия, меди и стали построены такие диаграммы. С их помощью можно рассчитать силу сопротивления деформированию для каждого конкретного металла или сплава. Таким образом, эта сила в основном зависит от механических свойств материала прокатываемой полосы.

Но при прокатке происходит в основном сжатие металла между валками, а не растяжение. Предположим, что мы сжали валками полосу толщиной h_о и шириной В на величину Dh и зафиксировали силу F_c, которая нам для этого потребовалась. На рисунке 4 результаты нескольких таких опытов представлены в виде графика зависимости силы F_c от толщины полосы h. Эта зависимость уже не линейная, так как происходит пластическая деформация полосы. Сила F_c - это, с некоторыми допущениями, не что иное, как сопротивление деформированию полосы. Давайте подумаем, как нам поступить дальше.

С одной стороны, на основании опытов, проведенных на прокатном стане без полосы, мы нашли жесткость стана. С другой стороны, на основании опытов по сжатию полосы в валках мы нашли величину ее сопротивления деформированию. Теперь мы можем ответить на поставленный ранее вопрос: какой зазор S_о
следует установить между валками, чтобы получить толщину полосы, равную h₁. Предположим, что мы хотим получить полосу толщиной h₁ на прокатном стане, жесткость которого определяется значением tg a из рисунка 3. Для этого сначала мы должны найти по графику зависимости F_c(h) силу сопротивления деформированию полосы, соответствующую ее прокатке от толщины h_o до h₁. Далее необходимо эту силу приравнять силе упругости стана (согласно третьему закону Ньютона) и с учетом жесткости стана определить необходимую величину зазора S_о.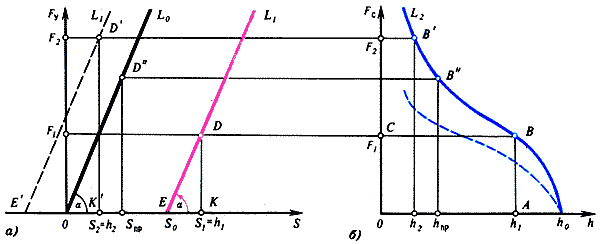

Рис. 5

Рисунок 5 проясняет, как проводится эта операция. На рисунке даны совместно графики зависимости F_y(S) и F_c(h). Из точки А на рисунке 5, б восстановим перпендикуляр до пересечения с кривой L₂ (точка В). Из точки В проведем горизонталь до пересечения с перпендикуляром, восстановленным из точки К (рисунок 5, a), соответствующей величине S₁ зазора между валками, который будет равен толщине полосы h₁ (S₁ = h₁). Через точку D пересечения горизонтали BD и вертикали KD проведем прямую L₁, параллельную L_o и определяющую пружину прокатного стана с заданной жесткостью tg a. Тогда точка Е пересечения прямой L₁ с осью S и дает нам необходимую величину S_о зазора между валками, который следует установить перед прокаткой, чтобы получить заданную толщину полосы, равную h₁.

Предположим теперь, что нам надо получишь полосу толщиной h₁ (см. рисунок 5, б). Проведя аналогичные рассуждения, мы окажемся в точке Е', что соответствует отрицательному зазору между валками. Следовательно, такой процесс прокатки мы осуществить не сможем и данный прокатный стан позволяет в пределе получить минимально возможную толщину полосы, равную h_пр.. Таким образом, для каждого прокатного стана есть своя предельная минимальная толщина полосы, зависящая в основном от свойств прокатываемого металла и размеров полосы. Полосу с толщиной меньше этой предельной на данном стане получить нельзя. А если нужна более тонкая полоса?

Посмотрите на рисунок 5. Увеличивая угол a, можно уменьшать предельно возможную толщину полосы. Значит, надо увеличить жесткость стана, в первую очередь - жесткость валков, так как доля их деформации в упругой деформации всего стана очень велика. Мы уже говорили, что этого можно добиться, используя опорные валки, число которых в реальных станах достигает восемнадцати (по девять на каждый рабочий валок).

Как вы догадываетесь, консервные банки отнюдь не основная продукция, которую изготовляют из стальной полосы. Например, для кинескопов цветных телевизоров нужна полоса из специальной стали толщиной 0,15 мм с допустимыми отклонениями от этой толщины ±:3 мкм. Конечно, технология получения такой полосы существенно отличается от технологии получения полосы для изготовления консервных банок. Более жесткими являются и прокатные станы.

При изготовлении конденсаторов и прокладок в магнитных головках для малогабаритной аппаратуры необходима фольга (тончайшая лента) из алюминия, тантала и бериллиевой бронзы толщиной 1-3 мкм. Как получить такую ленту? Надо отметить, что она, как правило, довольно узкая, 400-600 мм по ширине (в то время как полоса для консервных банок достигает 1,5 м в ширину). Конечно, для более узкой полосы сопротивление деформированию меньше, чем для широкой. Для прокатки такой узкой и тонкой ленты используют чрезвычайно жесткие двадцативалковые прокатные станы; прокатка производится в двух рабочих валках длиной 400-1200 мм, каждый из которых опирается на пирамиду из опорных валков. А вообще станы листовой прокатки определяются , длиной валка (шириной полосы); так что когда говорят "стан 1700", то это означает, что длина рабочей части валков 1700 мм.

Есть еще один путь уменьшения предельно возможной толщины полосы. Он сводитсй к изменению формы кривой L₂ (см. рисунок 5, б), т. е. к уменьшению силы сопротивления деформированию. Этого можно достигать различными путями: изменением условий трения между валками и полосой с помощью смазок, натяжением полосы во время прокатки, уменьшением ее ширины и другими способами. Проводят определенную термическую обработку металла (отжиг), снижающую сопротивление деформированию, что, кстати, широко используется при производстве ленты для кинескопов.

Однако все мероприятия, связанные с повышением жесткости стана и уменьшением сопротивления деформированию, как правило, связаны с дополнительными затратами. Так, полоса для кинескопов стоит значительно дороже полосы, идущей на изготовление консервных банок. Стоимость тончайших лент из некоторых металлов иногда в 20 раз больше стоимости золота той же массы. Вот и нужно думать: что выгоднее - прокатывать более толстую и более дешевую жесть или более тонкую и более дорогую. Очевидно, в каждом конкретном случае нужно исходить из реальных возможностей.

Не так давно на Карагандинском металлургическом комбинате пущен в эксплуатацию новый стан, позволяющий получать жесть толщиной 0,18 мм. Для консервных банок начинает использоваться тонкий лист из алюминиевых сплавов. Сопротивление деформированию при прокатке алюминия значительно ниже, чем при прокатке стали. Так что вопрос с консервными банками будет решен. Но дело, как мы уже говорили, не только в консервных банках, хотя без них иногда не обойтись. Дело в другом. Проблема деформаций инструмента при обработке металлов давлением является очень серьезной проблемой. В нашем случае инструментом были валки, и прокатка - один из процессов обработки металлов давлением. Таких процессов существует очень много, и они постепенно вытесняют обработку металлов резанием, так как более экономичны и малоотходны. Однако точность размеров изделий при обработке давлением, особенно в холодном состоянии, существенным образом зависит от жесткости инструмента и самих обрабатывающих агрегатов. Задача повышения жесткости еще далека от решения и ждет своего часа.