© С.Я. ГегузинаЯков Евсеевич Гегузин
КАПЛЯ
Воспроизведено по изданию
Я.Е. Гегузин, "Капля" (Научно-популярная серия АН СССР),
2-ое доп. изд., М., "Наука", 1977 г.
|
|
|
Глава 1 КАПЛЯ В НЕВЕСОМОСТИ
Опыт Плато
В условиях невесомости все выглядит так же, как и в условиях весомости, за исключением отсутствия веса, в связи с чем в условиях невесомости все выглядит не так, как в условиях весомости. Ответ на экзамене по физикеЖозеф Антуан Фердинанд Плато, профессор Гентского университета по кафедре физики и анатомии, в течение жизни занимался множеством различных проблем, которые, судя по всему, считал значительно более важными, чем поставленный им опыт с "невесомой" каплей. Но история рассудила иначе и прочно соединила его имя именно с этим опытом. Опыт широко известный, классический, демонстрируемый почти во всех лекционных курсах физики. В прозрачный сосуд наливается водный раствор спирта, и затем туда с помощью пипетки вводится капля масла. Концентрацию раствора можно сделать такой, чтобы плотность раствора и масла была одинаковой. В этом случае капля масла, не растворяющаяся в спиртовом растворе, вне зависимости от ее объема приобретет форму сферы и повиснет в растворе. Аналогичный опыт можно поставить, воспользовавшись соленой водой и кусочком жидкой эпоксидной смолы или анилина, - результат будет тот же.
Рис. 1. Капли анилина, взвешенные в воде, имеют сферическую форму вне зависимости от их размера Сферическая форма капли в опыте Плато объясняется тем, что вследствие равенства плотности вещества капли и среды сила тяготения, действующая на каплю, оказывается равной выталкивающей архимедовой силе. Именно поэтому капля не расплющивается и ее форма определяется только стремлением к уменьшению поверхностной энергии на границе капля-среда.
Плато, оставаясь приверженным Земле, поставил жидкость в условия, при которых капля оказывается как бы в невесомости, в условия, когда одна из особенностей поведения капли в истинной невесомости отчетливо себя проявила.
Здесь, пожалуй, следует истолковать смысл слов "как бы в невесомости".
Истинная невесомость - состояние, при котором тело движется только под действием сил всемирного тяготения. Падающий камень или падающая капля воды находятся в состоянии истинной невесомости без оговорки "как бы", поскольку все атомы, из которых они состоят, в равной мере свободно падают и сила тяжести не вынуждает их оказывать давление друг на друга. Свободно падающую каплю силы тяжести не расплющивают, и ее форму определяют только силы поверхностного натяжения. А в опыте Плато сила тяжести не исключена, но благодаря действию архимедовой силы она не расплющивает каплю, форму ее определяют силы поверхностного натяжения. Если каплю Плато попытаться взвесить, весы покажут нуль, поглядеть на нее - сферическая, как в невесомости, и все же слово "как бы" надо иметь в виду. Капля Плато подобна человеку, который, набрав в легкие воздух, не тонет в воде, не находясь при этом в невесомости: его кровеносная система, вестибулярный аппарат и прочие органы чувствуют действие силы тяжести. От истинной невесомости капля Плато заимствовала лишь сферическую форму. Она как бы в невесомости.
Истинная форма капли определяется суммой всех сил, которые на нее действуют, и поэтому задачи о форме капли в обычных условиях, как правило, очень сложны. Если капля лежит на твердой поверхности, то надо учесть и действие силы тяжести, которое будет каплю расплющивать, и действие собственного поверхностного натяжения, которое будет каплю сжимать, и действие поверхностного натяжения на границе капля - твердая поверхность, которое тоже в какой-то степени деформирует каплю. В опыте Плато действует только одна сила - обусловленная собственным поверхностным натяжением, и капля принимает форму сферы, т е. форму, которая при данном объеме отличается минимальной поверхностью.
Последнее утверждение обычно повторяют как само собой разумеющееся. Между тем стоило бы убедиться в том, что шар действительно обладает минимальной поверхностью. Это можно сделать с помощью рассуждений, некогда предложенных немецким геометром Штайнером. Воспроизведем его рассуждения в виде двухэтапной последовательности.
Этап первый. Фигура, поверхность которой минимальна при данном объеме, не может иметь вогнутые участки, так как превращение этих участков в плоские приводит к уменьшению поверхности, которое сопровождается увеличением объема.
Этап второй. Пересечем двусторонним зеркалом выпуклую пространственную фигуру так, чтобы поверхности слева и справа от зеркала были равны. Отразим в зеркале ту часть фигуры, объем которой оказался большим. При этом возникает симметричная фигура. Ее поверхность равна начальной, а объем увеличен. Таким образом, вследствие зеркального отражения мы "улучшили" фигуру, сделали ее более совершенной в том смысле, что увеличили ее объем, сохранив поверхность. Единственная фигура, которую последовательностью зеркальных отображений невозможно "улучшить", т.е. объем которой будет максимальным при данной поверхности или поверхность - минимальной при данном объеме, будет сфера. Это именно то, в чем мы и хотели убедиться.
Результат опыта Плато не зависит от размера капли. Любая капля в невесомости будет сферической. Легко, однако, убедиться - и с помощью расчета, и с помощью опыта, - что форма капли может оказаться близкой к сферической и в том случае, если она не находится в невесомости. Для этого капля должна быть настолько мала, чтобы ее вес не мог заметно исказить сферическую форму, которую ей стремится придать поверхностное натяжение. Попытаемся определить, какую каплю в этом смысле следует считать "маленькой". Для этого надо сравнить два давления: то, которое придает капле форму сферы, и то, которое ее расплющивает. В случае "маленькой" капли второе давление должно быть значительно меньше первого.
Первое давление - оно называется капиллярным, или лапласовским, - определяется хорошо известной формулой Pp = 2a/R ~1/R, в которой a - поверхностное натяжение, a R - радиус капли. Это давление, возрастая с уменьшением размера капли, в случае очень маленьких капель может быть огромным. Учтя, что поверхностное натяжение воды a = 70 дин/см, легко убедиться, что микроскопическая водяная капелька, радиус которой одна сотая микрона (R = 10-6 см), сжата лапласовским давлением, величина которого около 150 атмосфер!
Теперь о давлении, которое расплющивает лежащую каплю. Назовем его гравитационным Pg. Величину этого давления, равного отношению силы тяжести капли, масса которой m, к площади контакта между каплей и твердой поверхностью, точно определить трудно, потому что неизвестна величина этой площади. Его можно оценить, посчитав, что площадь контакта приблизительно равна квадрату радиуса капли. В этом предположении Pg » mg/R2, где g - ускорение силы тяжести. Так как масса капли m = 4/З pR3r, где r - плотность вещества, из которого она состоит, то Pg » 4/З pRgr ~ R. Итак, с уменьшением капли Pp растет, а Pg убывает, и, следовательно, должен быть такой размер капли, ниже которого Pp будет превосходить Pg. И если Pp >> Pg, форма капли должна подчиниться давлению Pp, т.е. стать почти сферической. Это будет в случае "маленьких" капель, радиус которых должен удовлетворять неравенству R << (3a / 2prg)1/2, следующему из неравенства давлений. Итак, "маленькой" мы будем считать каплю, для которой лапласовское давление существенно превосходит гравитационное. Или иначе: гравитационное давление, вызванное условиями "весомости", столь мало по сравнению с лапласовским, что капля себя ведет так, будто она находится в невесомости.
Все рассуждения о почти сферической форме "маленькой" капли могут совершенно потерять смысл, если силы поверхностного натяжения на границе капля - твердая поверхность растянут каплю, заставят ее растечься тонким слоем. Однако во многих случаях, когда капля не смачивает подложку, наши рассуждения остаются в силе. Именно такие случаи мы и обсуждали.
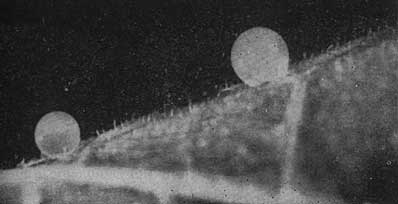
Рис. 2. "Маленькие" водяные капли на ворсистой поверхности листа
чувствуют себя почти в невесомости"Маленькие" капли совершенной формы можно наблюдать после дождя на листьях многих деревьев. Не смачивая лист, капли располагаются на нем сверкающими шариками. Особенно хороши они на тыльной, ворсистой стороне. Капли висят как бы в воздухе, поддерживаемые ворсинками. Прекрасные "маленькие" капли можно увидеть после дождя на кончиках игл кактуса или ели.

Рис. 3. В невесомости между электродом и сварным швом
формируется почти сферическая капляВернемся к капле, находящейся в невесомости. Советский космонавт В. Н. Кубасов наблюдал жидкие капли в условиях невесомости. Он производил опыты по электросварке плавящимся электродом в космосе. Процесс сварки был запечатлен на кинопленке. Оказалось, что на кончике электрода формируется большая, почти сферическая капля жидкого металла, существенно больше той, которая образуется при сварке в земных условиях. Капли жидкого металла, случайно оторвавшиеся от электрода, свободно парят около места сварки, подобно тому как движутся капли в опыте Плато, если их слегка толкнуть.
Творческая фантазия Плато более 100 лет назад родила идею наземного опыта с каплей, в котором она вела себя как бы в невесомости. Быть может, он тогда думал и о космосе?
Воспоминание о лекции профессора Френкеля
Начну с банальной мысли о том, что впечатления юности запоминаются надолго - в звуках, в цвете, в незначащих деталях, которые тогда, в давно прошедшие годы, казались особенно важными.
Лекцию Якова Ильича Френкеля я слушал поздней весной 1939 г. Он тогда приезжал в Харьков и в маленькой университетской аудитории амфитеатром, которая еще с середины прошлого века торжественно называлась "большой физической", читал лекцию о капельной модели ядра. Теперь, спустя более трети века, когда во всех подробностях известны драматические события тех дней, когда закладывались основы ядерной энергетики, ясно, что с профессором Френкелем, который всего за несколько недель до приезда в Харьков предложил идею капельной модели ядра, в аудиторию вошла сама история. Тогда же мы, студенты-физики, шли слушать очередную лекцию "гостевого" профессора, одну из многочисленных лекций, которые в "большой физической" часто читали нам университетские гости.
Начал лекцию Френкель спокойно, размеренно, но постепенно академическая размеренность исчезла: он говорил так, как можно говорить лишь о самом сокровенном, о чем непрерывно думаешь, и кажется, что открывшееся тебе прозрение и ясность абсолютно необходимо передать слушателям. Именно на этой лекции я понял смысл выражения "слушать, затаив дыхание". Затаив, возможно, для того, чтобы не было лишних звуков, а возможно, чтобы не отвлекаться для дыхания.
Формул профессор почти не писал. Нарисовав мелом на доске водопроводный кран с набухающей каплей на конце, он начал рассказывать об аналогии между каплей воды и каплей ядерной жидкости - атомным ядром. До достижения некоторого размера капля на кончике крана устойчива: по крану можно щелкнуть, и капля не оборвется (он щелкнул по нарисованному крану). Когда же, набухая, капля достигнет определенного размера, она сама оборвется. И неожиданно заключил: периодическая система потому и оканчивается на уране, что тяжелая капля ядерной жидкости - ядро урана - велика и находится на пределе устойчивости, подобно той капле воды на кончике крана, которая вот-вот оторвется от него. Когда после этого, как само собой разумеющееся, он предсказал возможность спонтанного деления ядра урана, возникло ощущение провидения.
Теперь, когда мне на лекциях приходится рассказывать студентам о ядре, я ловлю себя на том, что невольно пытаюсь повторять фразы и рисовать картинки, которые отпечатались у меня в памяти после той далекой предвоенной лекции, слышанной в юности.
Термин "деление" применительно к ядру впервые использовала Лизе Майтнер - выдающийся немецкий физик. Она, однако, имела в виду аналогию не с каплей, а с амебой. Аналогия со сферической каплей, которая не деформируется тяжестью, оказалась значительно более глубокой и содержательной.
Естественно возникает вопрос, где основания для аналогии? Ведь недостаточно представить себе, что, подобно жидкой капле, ядро имеет форму шарика. Видимо, Френкель усмотрел в строении ядра более глубокие основания, чтобы уподобить его жидкой капле.
Поиски аналогий - потребность многих умов, пробивающихся сквозь сплетения идей и фактов, сквозь заросли отрывочных наблюдений. Удача в этих поисках, как известно, зависит не только и, быть может, не столько от эрудиции и способности мыслить формально строго - она зависит от умения из множества жизненных наблюдений, из хранящихся в тайниках мозга некогда подмеченных штрихов явлений и событий в нужный момент извлечь именно те, которые наиболее полно походят на осмысливаемое явление или образ. Это совершенно естественная попытка мозга - среди известного, понятного, ставшего "своим", отыскать нечто такое, чему незнаемое уподобится, а уподобившись, потеряет загадочность и тоже станет "своим".
Иной сочтет поверхностное сходство достаточным основанием для аналогии - такому путь к откровениям заказан. Поверхностная аналогия не ведет к знаниям, а хитро уводит от них. Какая же аналогия окажется глубокой? Как и чем измеряется ее глубина? Чем руководствоваться, чтобы не принять внешнее сходство за истинную аналогию? У одного из восточных народов в ходу мудрость: "С нетерпением ожидая возвращения дорогого друга из военного похода, не ошибись, не прими стук своего сердца за топот копыт его коня". Как же не ошибиться? А ведь очень часто интуиция - именно ей и принадлежит основная инициатива отбора в кладовых памяти всего подходящего к случаю - вместо истинной и глубокой аналогии предлагает нам, образно выражаясь, троянского коня. В словаре русского языка в качестве синонима слова "интуиция" называется слово "чутье". Так вот "чутьем" профессор Френкель был богато одарен. В этом смысле он был богачом.
Об аналогии между атомным ядром и каплей жидкости, вернее о том, в чем он усматривает основания для аналогии, Френкель говорил так просто и естественно, будто она не была угадана его чутьем, а заведомо очевидна любому студенту. Говорил доверительно, не низводя слушателя до положения школяра, которого известный ученый одаривает крупицами своих необозримых знаний, вынуждая себя при этом опуститься до школярского уровня. Он очень умело создавал иллюзию разговора "на равных" со слушателем, который чувствует себя вправе перебить лектора, усомниться в его правоте, выразить одобрение.
Силы притяжения, говорил он, которые удерживают протоны и нейтроны в ядре, велики и могут противостоять силам электрического отталкивания, действующим между протонами в ядре. И это несмотря на то, что расстояния между протонами ничтожно малы, около 10-13-10-12 см. Сравнив энергии различных ядер и их геометрические размеры, можно убедиться, что силы, удерживающие нейтроны и протоны в ядре, в одном существенном отношении сходны с обычными силами межмолекулярного взаимодействия в жидкостях, а именно в том, что эти силы "короткодействующие". Они значительны лишь на расстояниях, сравнимых с размерами частиц - протонов и нейтронов в ядре и молекул в обычной жидкости. Различия между ядерными силами и силами взаимодействия между молекулами в жидкости заключаются в том, что радиус действия у первых в сто тысяч раз меньше, чем у вторых, а определяемая ими энергия связи - в миллион раз больше. Различие, разумеется, огромное, но только количественное, а не качественное, и аналогии оно не помеха.
Френкель обратил внимание на то, что объемы различных ядер оказываются пропорциональными их массе, т.е. атомному весу соответствующих элементов. А это означает, что ядерное вещество, как и обычная жидкость, имеет постоянную плотность, которая от размеров ядра не зависит. Вот теперь есть основания говорить о ядерной жидкости, о ядре-капле. Плотность этой жидкости, говорил лектор, можно вычислить, и она оказывается в биллионы раз больше плотности обычных жидкостей, поверхностное натяжение - в 1018 раз больше поверхностного натяжения воды.
Не многим дано увидеть черты сходства между веществами, характеристики которых различаются в такое число раз, а профессор Френкель увидел, и его интуиция не отступила перед числом с 18 нулями.
Аналогия - это значит не тождество, а аналогия, и где-то ей положен предел. И ядерная жидкость не тождественна обычной. Ядра, капли ядерной жидкости, в отличие от капель жидкости обыкновенной, имеют электрический заряд, связанный с входящими в их состав протонами. Вот это отличие принципиальное, а не количественное, и оно определяет одно своеобразное свойство ядер-капель, которым не обладают обычные капли, дождинки или росинки. Именно это отличие и кладет предел аналогии.
Представим себе в невесомости две капли: одну из обычной жидкости, вторую - из ядерной. Невесомость нам нужна только для того, чтобы силы тяжести не искажали их форму. Будем мысленно увеличивать объем этих капель. С первой из них, "обычной", это можно делать без всяких ограничений - ее форма будет оставаться сферической. Жидкость в капле будет подвержена лишь давлению всестороннего сжатия, которое обусловлено кривизной ее поверхности. А вот со второй каплей, ядерной, дело обстоит сложнее. Ее вещество электрически заряжено. Это значит, что полусферы, на которые капля может быть условно разделена, взаимно отталкиваются, подчиняясь закону Кулона, согласно которому силы отталкивания прямо пропорциональны произведению взаимодействующих зарядов и обратно пропорциональны квадрату расстояния между ними. Так как величина заряда каждой из ядерных полусфер пропорциональна их объему, т. е. кубу радиуса, а расстояние между ними - радиусу, то, очевидно, с увеличением объема капли силы отталкивания, которые пытаются исказить сферическую форму капли, будут расти и в конечном счете разорвут ее. Препятствует этому лапласовское давление, которое стремится придать капле сферическую форму. Это давление, однако, с увеличением капли убывает. Сколь бы малым оно ни было, в условиях невесомости его всегда будет достаточно для того, чтобы капля обычной жидкости оставалась сферической, а в случае заряженной капли с лапласовским давлением вступает в борьбу иное давление, электростатическое, искажающее сферическую форму капли. Итак, два давления. Одно с увеличением размера капли падает, а другое - растет. И, следовательно, это другое в конце концов окажется победителем: под его влиянием капля деформируется и разорвется на две разлетающиеся маленькие капли.
Профессор Френкель об этом говорил так. Деление ядра капли на две дочерние капли осуществляется не сразу, а путем постепенного вытягивания, при котором оно сначала превращается в вытянутый эллипсоид, затем центральное сечение этого эллипсоида сужается, образуя шейку. Шейка постепенно утоньшается, пока, наконец, не разорвется, после чего процесс деления может считаться законченным. Разумеется, и вытягивание, и последующий разрыв происходят в режиме колебаний ядра-капли, во время одного из периодов этих колебаний, когда изменение формы капли оказалось наиболее значительным.
На доске появились элементарные формулы: Френкель "оценивал" атомный вес того элемента, ядро которого должно потерять устойчивость и разделиться на два дочерних. Атомный вес такого элемента оказался близким 100. Оценка озадачивающая, так как если она верна, то все элементы, атомный вес которых больше 100, должны были бы потерять право на существование, а в периодической системе элементов фигурируют более тяжелые элементы, вплоть до урана, атомный вес которого 238. Что-то, видимо, в оценке не учтено. Что же? Френкель уже говорил о том, что, превращаясь в две сферические дочерние капли-ядра, материнское ядро должно постепенно вытягиваться. Это значит, что поверхность, а с ней и поверхностная энергия должны увеличиваться. Следовательно, на пути к процессу деления природой поставлен барьер, который необходимо преодолеть. Величину этого барьера можно вычислить, и во время лекции профессор это сделал. Он показал, что по мере увеличения радиуса материнского ядра-капли этот барьер постепенно снижается и становится практически равным нулю для ядра урана. Вот почему все, что можно "примыслить" за ураном, не должно быть долго жизнеспособным, а менделеевская таблица "стабильных" элементов должна оканчиваться именно ураном.
Вернемся к водопроводному крану. Капелька, формирующаяся на его конце, подвержена действию силы тяжести, которая деформирует каплю. Действие ее подобно действию электростатических сил отталкивания между двумя половинками заряженного ядра. Таким образом, если усматривать аналогию между развалом ядра и отрывом капли от кончика водопроводного крана, надо домыслить, что в кране остается капелька, подобная той, которая от него оторвалась.
После лекции профессора Френкеля прошло более 30 лет. Капельная модель ядра уточнена, улучшена, а глубокая аналогия, навеянная видом капли на кончике крана или, быть может, дождевой каплей, в науке осталась прочно. Эта аналогия помогла решить задачи общечеловеческой значимости.
Образ капли близок творчеству Френкеля, к каплям он обращался много раз в разные годы и по разным поводам.
О подпрыгнувшей каплеВначале совсем очевидное утверждение: если в силу каких-либо обстоятельств капля приобрела несферическую форму, это означает, что ее поверхность увеличилась по сравнению с поверхностью сферы и, следовательно, увеличилась и ее поверхностная энергия. Или если в силу каких-либо обстоятельств несферическая капля вдруг приобретает сферическую форму, вследствие уменьшения поверхности должна выделиться избыточная энергия.
Допустим, что нам удалось осуществить преобразование формы капли от несферической к сферической, удалось предоставить возможность избыточной поверхностной энергии освободиться, выделиться. Кстати, эта энергия может оказаться совсем немалой. Ее очень легко вычислить, если задаться объемом капли и ее начальной формой. Вот пример, который дальше нам пригодится. Крупная капля ртути весом 20 г на стеклянной пластинке имеет форму лепешки, близкую к форме цилиндра, радиус которого 1,2 см, а высота 0,35 см. Если эта капля превратится в сферу, то при этом освобождается энергия W = 1060 эрг.
Куда же эта энергия денется, на что она способна, что может произойти после того, как капле эта энергия в качестве поверхностной станет не нужна? Какие процессы могут сыграть роль "стоков" выделившейся энергии? Очевидно, некоторая часть энергии должна будет израсходоваться на то, чтобы осуществить перемещение вещества капли, в результате которого капля станет сферической. Дело в том, что жидкость, из которой капля состоит, обладает некоторой вязкостью, и поэтому всякое изменение формы капли связано с необходимостью преодолеть сопротивление вязкой жидкости ее деформированию, т.е. с необходимостью совершить работу против сил внутреннего трения. Кроме того, часть освободившейся энергии может израсходоваться на нагрев капли. Можно ожидать, что, приобретая сферическую форму, капля будет сама себя подогревать. Кроме того, может нагреваться и пространство, окружающее каплю. В этом случае сфероидизирующаяся капля будет играть роль своеобразной печки, отапливающей пространство вокруг себя.
Кроме названных "стоков" для избыточной энергии можно указать еще один - в основном о нем далее и будет разговор. Если приплюснутая несферическая капелька лежит на твердой пластинке и если почему-либо она должна преобразовать свою форму из несферической в сферическую, можно ожидать, что в момент преобразования она оттолкнется от пластинки и подскочит вверх, как может подскочить каждый из нас, оттолкнувшись от земли. Для совершения такого скачка капля, естественно, нуждается в энергии, которая может быть частью энергии, выделившейся при сокращении поверхности капли.
Как видите, стоков энергии много, и, очевидно, все "работающие", но скорость их действия и "поглощательная способность", конечно, различны. Совершенно ясно, что капля не подпрыгнет, если изменение ее формы будет происходить медленно. В этом случае принципиально возможный расход энергии на скачок не произойдет. И на борьбу с сопротивлением жидкости изменению ее формы тоже будет расходоваться мало энергии, потому что этот расход, как оказывается, тем больше, чем быстрее должно произойти изменение формы. При медленной сфероидизации капли выделяющаяся энергия была бы израсходована в основном на ее нагрев и нагрев окружающего пространства. Увидеть, как капля подпрыгнет, можно лишь при условии, что преобразование ее формы будет происходить быстро. Если, присев на корточки, мы будем медленно распрямляться, прыжок не получится: чтобы подпрыгнуть, надо, быстро распрямляясь, оттолкнуться от земли. Но что значит "быстро" применительно к капле, которая изменяет свою форму? Капле, чтобы подпрыгнуть, надо побороть силу тяжести, препятствующую прыжку.
Итак, возникает задача, которую можно сформулировать следующим образом. Допустим, что вся энергия, которая выделяется в процессе сфероидизации капли, должна быть израсходована только на ее подпрыгивание. Пусть другие стоки энергии каким-то образом запрещены. Спрашивается, при какой длительности процесса преобразования формы капли в сферическую капля оторвется от твердой пластинки, на которой она лежит? Решить такую задачу просто. Это могут сделать восьмиклассники в начале учебного года, узнав, что кинетическая энергия тела равна половине произведения его массы на квадрат скорости (Wk = mv2/2), чтo сила, действующая на тело, равна произведению его массы на ускорение (F = mа) и что ускорение есть отношение изменения скорости к тому времени, за которое оно произошло (а = v/t). В нашем случае m - масса капли, а - ускорение, v - скорость подпрыгнувшей капли, находившейся перед прыжком в состоянии покоя, t - время, в течение которого произошло преобразование формы капли.
На каплю в момент ее прыжка действуют две силы. Одну из них мы уже упомянули: F1 = ma = mv/t - эта сила отрывает каплю от подложки. Сила тяжести, прижимающая ее к опоре, - F2 = m(g - g*), где g - и g* - ускорение силы тяжести и опоры соответственно. Прыжок может состояться, если F1 >> F2. Воспользовавшись приведенными формулами, легко убедиться в том, что капля подпрыгнет при условии, если время преобразования ее формы t < (1/(g - g*))(2Wk /m)1/2.
Напомним сделанное предположение: вся энергия, выделяющаяся при изменении формы капли, расходуется только на подпрыгивание. Именно поэтому в последней формуле надо считать, что Wk = W. Двадцатиграммовая ртутная капля, которая лепешкой лежит на покоящейся стеклянной пластинке, когда g* = 0, превращаясь в шар, выделяет энергию W =1060 эрг и сможет подпрыгнуть лишь при условии, если преобразование ее формы произойдет за время, меньшее чем одна сотая секунды.
При такой оценке времени кажется, что надежда наблюдать подпрыгивающую каплю становится иллюзорной. Но если каплю на подложке перевести в состояние невесомости, когда g* = g, произойдет то, к чему мы стремимся: капля начнет приобретать сферическую форму даже при сколь угодно медленном преобразовании ее формы. При малейшем изменении формы она оторвется от пластинки и с некоторой скоростью начнет двигаться от нее. Ситуация совершенно аналогична той, в которую попадают космонавты во время полета, когда им приходится специально заботиться, чтобы случайное движение не вынудило их покинуть рабочее место.
Вот теперь можно рассказать о великолепном эксперименте, который в 1970 г. поставили советские физики И.М. Кирко, Е.П. Добычин и В.И. Попов. Их эксперимент состоял в следующем. Тяжелый контейнер, в котором располагались прозрачный сосуд с 20-граммовой каплей ртути, залитой раствором соляной кислоты, и автоматически работающая кинокамера, сбрасывался с высоты 20 м. Во время свободного полета, длившегося 2 сек., все содержимое контейнера было практически в состоянии невесомости. Кинокамера зафиксировала происходящее в полете: ртутная лепешка, превращаясь в сферу, подпрыгнула и полетела прочь от дна прозрачной кюветы со скоростью 8,7 см/сек. Это главное наблюдение, сделанное камерой. Проверим, как оно согласуется с величиной энергии, которая должна выделиться при сфероидизации капли. Именно для этой проверки в начале очерка была названа энергия, которая выделяется при сфероидизации ртутной капли весом 20 г. Получив скорость 8,7 см/сек., она унесет с собой энергию Wk = mv2/2 = 752 эрг, т.е. большую часть выделяющейся энергии. Не использованными при прыжке остались 1060 - 752 = 308 эрг. Как показала кинокамера, основная часть этой энергии была израсходована на преодоление сопротивления вязкой ртути ее деформированию: движущаяся капля пульсировала, колебалась, и на это расходовалась энергия.

Рис. 4. Подпрыгнувшая в невесомости капля, колеблясь, свободно летит вверх
При опытах обнаружился еще один сток энергии - на этот раз энергии движущейся капли. Когда капля подходила к границе соляная кислота - воздух, граница изгибалась и отражала от себя каплю, заставляя ее двигаться в обратном направлении. Часть энергии капли расходовалась на изгиб границы. Ртутная капля, подобно мячику, металась между дном кюветы и границей между соляной кислотой и воздухом. Именно поэтому свою статью, опубликованную в "Докладах АН СССР" (1970, т. 192, № 2), экспериментаторы назвали не совсем академично, но точно и выразительно: "Явление капиллярной игры в мяч в условиях невесомости".
Возникает естественный вопрос: почему этот опыт, в основе своей "классический", постановка которого не предполагает использования каких-либо новых "квантовых" идей, не был осуществлен, скажем, 150 лет назад? Неужели потому, что тогда не было автоматических кинокамер? Но мог же какой-нибудь энтузиаст-естествоиспытатель, держа в руках перед глазами прозрачную кювету с ртутной лепешкой, покрытой соляной кислотой, прыгнуть "солдатиком" в воду с десятиметровой вышки! Вынырнул бы и сообщил, что капля подпрыгнула. И скорость ее мог бы определить по зарубкам на кювете. А вот не прыгнул. Видимо, не было интереса к тому, что может произойти в невесомости. А сейчас, в наш век, интерес к невесомости огромный. Вот и пришла в голову мысль сбросить с высоты контейнер с ртутной каплей и автоматической кинокамерой.
Фильм о слиянии двух капельЭтому фильму предшествовала 26-летняя история. Ее начало восходит к 1944 г., а фильм был снят в 1970-м. Прежде чем всмотреться в кадры фильма, пожалуй, стоит проследить этапы этой истории. Началась она в Казани. Я.И. Френкель был в этом городе в эвакуации и работал над развитием теории жидкости и твердого тела. Он обдумывал вопрос, который и до него возникал перед многими: каким образом твердые, скажем металлические, порошинки, которые соприкасаются лишь в отдельных точках, после длительного отжига при высокой температуре оказываются прочно соединенными, приблизившимися друг к другу, - вопрос, рожденный необходимостью понять физику процессов, которые происходят при спекании спрессованных порошков, процессов, лежащих в основе порошковой металлургии.
Ученый последовательно развивал мысль: в строении твердых и жидких тел много общих черт и процесс плавления не бог весть какое революционное событие в жизни вещества, так как плотность при этом изменяется незначительно, незначительно меняется и расстояние между атомами, а следовательно, и силы, связывающие их. При плавлении катастрофически уменьшается вязкость вещества - жидкость течет даже при малых воздействиях на нее, а твердое тело при таких воздействиях зримо остается неизменным, сохраняя свою форму. В действительности, однако, и оно течет, но это происходит во много раз медленнее, чем в жидкости.
Такое различие свойств жидкости и твердого тела Френкель считал не принципиальным, а только количественным. В кругу этих идей у него и появился ответ на вопрос о том, каким образом твердые порошинки при высокой температуре самопроизвольно сближаются и соединяются в одно целое. Они просто сливаются, подобно тому как сливаются две соприкоснувшиеся жидкие капли. Такое слияние и в случае твердых крупинок, и в случае жидких капель оправданно и выгодно потому, что сопровождается уменьшением поверхности порошинок-капель. Вот, пожалуй, основная идея: порошинки сливаются, и этот процесс приводит к выигрышу энергии. Теперь нужен расчет скорости процесса слияния капель или крупинок. Он завершится формулой, затем эту формулу следует вручить экспериментатору, который выступит третейским судьей между теоретиком и явлением.
Профессор Френкель как-то писал о том, что хороший теоретик обычно рисует не точный портрет явления, а карикатуру на него. Это значит, что, подобно карикатуристу, он отбрасывает не очень существенные детали явления и оставляет лишь наиболее характерные его особенности. Талантливый карикатурист нарисует несколько завитков на лбу, кончики пальцев, держащих сигару, узел галстука - и все уже знают, кого он изобразил. Перед физиком-теоретиком почти та же задача. Реальное явление, как правило, очень сложно и описать его абсолютно точно чаще всего просто немыслимо. И Френкель, великолепный теоретик, нарисовал "карикатуру" процесса: вместо реальных крупинок произвольной формы он примыслил две сферические крупинки, вместо реального контакта по какой-то сложной поверхности - контакт в одной точке. И еще одно упрощение он вынужден был сделать: решил описать лишь начальную стадию процесса, когда на образование контактного перешейка между двумя каплями расходуется так мало вещества, что радиусы сливающихся капель можно считать практически неизменившимися. Он считал, что на этой стадии слияние сферических капель происходит под действием сил, которые приложены только к вогнутым участкам поверхности формирующегося перешейка, движутся только эти участки поверхности, а вся прочая поверхность сфер в процессе участия не принимает.
Теоретик сделал главное: предложил идею и определил условия, в которых проявляются наиболее существенные черты явления. После этого формула появилась без особого труда. Оказалось, что площадь круга, по которому соприкасаются сферические капли, равномерно увеличивается со временем: время увеличилось вдвое и площадь - вдвое, время - втрое и площадь - втрое.
Неизвестно, заботился ли Френкель лишь об удобствах теоретика, определяя черты "карикатуры", или думал и об экспериментаторе, но модель сливающихся сферических капель была экспериментаторами охотно взята "на вооружение". Они припекали друг к другу маленькие стеклянные бусинки, нагретые до высокой температуры. Подчеркнем слово "маленькие" - сферические бусинки имели диаметр не более долей миллиметра. С бусинками более крупными экспериментировать нельзя, так как они будут деформироваться под влиянием собственной тяжести, а этого модель Френкеля не предусматривает. Специально не подчеркивая этого, Френкель предполагал, что капли подвержены лишь силам, которые обусловлены наличием поверхностного натяжения.
Опыт ставился следующим образом: соприкасающиеся бусинки выдерживались при высокой температуре некоторое время, затем охлаждались. На охлажденных бусинках измерялась ширина контактного перешейка, а потом все повторялось сначала: нагревались, выдерживались, охлаждались, измерялись. В каждом таком цикле добывалась одна экспериментальная точка. По 5-10 точкам строилась зависимость квадрата ширины контактного перешейка (эта величина пропорциональна площади контакта) от времени. Экспериментальные точки не совсем точно укладывались на прямую, но в общем, как и предсказывает формула Френкеля, прямая получалась.
Итак, как будто круг замкнулся. Экспериментатор подтвердил правоту теоретика, узнал в "карикатуре" истинную натуру. И все же, может быть, он увидел не все? Возможно, согласие теории и эксперимента иллюзорно, оно не точное, а, как говорят, "в общих чертах". Теоретику, определившему задачу, те допущения, которые он делает, решая ее, "карикатура" простительна, а от экспериментатора можно потребовать подлинную фотографию с деталями, которые не обязательны в "карикатуре".
Опыты с микроскопическими бусинками - не лучшим образом поставленные опыты. Во-первых, бусинки малы, и поэтому некоторое изменение их формы в процессе взаимного слияния обнаружить непросто. Во-вторых, они не абсолютно сферические. В-третьих, пусть немного, но сила тяжести все же искажает форму бусинок, размягченных температурой. В-четвертых, 5-10 точек, рассеянных вокруг прямой,- не стопроцентная гарантия выполнимости предсказаний теоретика.
Теперь уместно перейти к фильму о слиянии двух капель. Он назван "Слияние вязких сфер". Чтобы избавиться от перечисленных упреков в неточности, опыт, который должен был быть заснят на кинопленку, мы поставили так.
Два одинаковых по весу бесформенных кусочка вязкого вещества, допустим смолы, следует поместить в жидкость, плотность которой в точности совпадает с плотностью смолы. Вскоре, если температура жидкости достаточна, бесформенные кусочки превратятся в идеальные сферы, как это было в опыте Плато. В этом случае не следует бояться, что сила тяжести исказит форму сфер. Это дает экспериментатору возможность изучать не микроскопические бусинки, а крупные сферы. Снимая этот фильм, мы экспериментировали со сферами диаметром 5 см. Разобщенные сферы приводились в контакт, и все происходящее с ними снималось кинокамерой. Две пятисантиметровые сферы сливались в одну приблизительно за 1 мин. Так как скорость съемки - 24 кадра в секунду, то весь процесс оказывался запечатленным на огромном количестве кадров - более тысячи. Для игрового фильма это число кадров ничтожно, а для экспериментатора 1000 кадров - это 1000 экспериментальных точек! По этим точкам можно построить надежную кривую, отражающую зависимость изучаемой характеристики от времени. Наблюдая за слиянием сфер в описанном опыте с помощью кинокамеры, можно получить истинный "портрет" явления и оценить интуицию и зоркость теоретика.
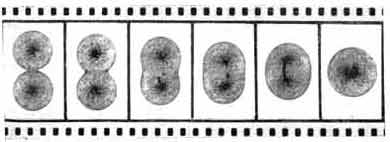
Рис. 5. Слияние капель эпоксидной смолы
Кадры фильма свидетельствуют о том, что в основном Френкель был прав, но только в основном. Действительно, быстрее иных участков поверхности движется вогнутая поверхность контактного перешейка, но движется не только она. Оказывается, что, стремясь поскорее слиться, сферы меняют свою форму и рядом с перешейком. Поэтому центры сфер сближаются быстрее, чем это следует из расчетов Френкеля. Поэтому и площадь контакта со временем изменяется по очень сложному закону, а закон, выведенный Френкелем, проглядывает сквозь последовательность огромного числа точек лишь как нечто усредненное, справедливое приближенно. На киноленте, кроме того, были запечатлены и более далекие стадии слияния сферических капель, которые описать с помощью формул чрезвычайно трудно. Начинает перемещаться вещество во всем объеме сферы, в каждой точке с разной скоростью и в разных направлениях, и оказывается практически невозможным усмотреть черты, пригодные для создания похожей "карикатуры".
Вот уже четверть века идея Френкеля определяет деятельность всех тех, кто занимается изучением процесса спекания. Кинокамера не отменила исследование 26-летней давности, а лишь указала на детали, от которых освободила сложное явление интуиция теоретика.
Статья Эйнштейна о лорде КельвинеВ конце 1924 г. в немецком журнале "Naturwissenschaften" появилась статья Эйнштейна "К столетию со дня рождения лорда Кельвина". Эйнштейн счел своим долгом почтить память лорда Кельвина - Томсона - выдающегося английского физика прошлого века. Статья начинается с характеристики Кельвина - "...один из наиболее сильных и плодотворных мыслителей XIX столетия...", "...основатель теоретической школы, из которой вышел гениальный теоретик нового времени К. Максвелл...", "...одаренный богатой фантазией, редким умением применять математический аппарат и проникновенным умом...", "...не многие ученые были столь же плодотворны". А затем - о конкретных заслугах и достижениях. "Наиболее существенный вклад Томсона в развитие физики - это основание термодинамики..."; "В возрасте 23 лет он вводит одно из фундаментальнейших понятий современной физики - абсолютную температуру..."; "обилие результатов... в области учения о теплоте, гидродинамики, учения об электричестве, навигации, физической географии и измерительной техники..."
В мемориальной статье Эйнштейн стремится принести дань глубокого уважения блестящему ученому и решает не писать обо всей деятельности Кельвина, а показать четкость его исследовательской мысли на нескольких примерах, которые в свое время Эйнштейна особенно восхитили. Из множества работ Кельвина он выбрал те, которые имеют касательство к каплям, вернее из трех работ Кельвина, особенно поразивших Эйнштейна, две оказались о каплях. Об одной из этих работ я лишь упомяну, а о второй - расскажу подробно.
В первой работе Кельвин предлагает идею генератора высокого напряжения, в котором главным работающим элементом являются капли. Им оказывается под силу перераспределять заряды между электродами и таким образом создавать огромную разность потенциалов.
Во второй работе Кельвин заинтересовался следующим вопросом: как зависит давление пара жидкости вблизи поверхности от степени ее искривленности? Если рассуждать предметно, то речь идет о том, насколько отличается давление пара вблизи изогнутой поверхности водяной капли от давления пара вблизи плоской поверхности воды, налитой в широкое блюдце.
Рис. 6. К расчету влияния кривизны поверхности жидкости на давление пара над ней В поисках ответа на этот вопрос Кельвин рассуждал так. Допустим, что в сосуд с жидкостью погружена тонкая трубка, внутренний радиус которой R. Если жидкость не смачивает материал, из которого сделана трубка, то ее уровень в трубке расположится ниже, чем в широком сосуде, в который налита жидкость. Произойдет это по причине очевидной: в связи с тем, что жидкость не смачивает стенок трубки, поверхность жидкости в ней будет выпуклой, полусферической, именно поэтому к жидкости будет приложено давление, направленное внутрь, то самое лапласовское давление, с которым мы уже встречались, обсуждая опыт Плато. Под влиянием этого давления уровень жидкости в трубке опустится ровно настолько, чтобы давление из-за разности уровней жидкости в трубке и вне ее в точности равнялось лапласовскому. Его величину мы знаем: Pp = 2a/R. Разность уровней h обусловит давление Р = rgh. Буквами обозначены следующие величины: a - поверхностное натяжение жидкости, r - ее плотность, g - ускорение силы тяжести. Приравняв два эти давления, мы убедимся, что разница уровней h = 2a/rgR. Таков результат первого этапа рассуждений Кельвина.
Второй этап рассуждений - продолжение первого. Над всей поверхностью жидкости - и той, которая в трубке, и той, которая в широком сосуде,- имеется пар этой жидкости, однако не везде давление, оказываемое им на жидкость, одинаково: несколько большим оно будет над поверхностью жидкости в трубке, так как слой пара над ней толще на величину h. Очевидно, дополнительное давление этого слоя равно DР = rogh, где ro - плотность газа, которая много меньше плотности жидкости. Величину h мы знаем - она была найдена на первом этапе рассуждений - и, следовательно, можем определить величину DР. Она очень важна, и поэтому формулу, которая определяет эту величину, мы вынесем на отдельную строку:
DР = (2a/R)( ro/r)
По поводу этой формулы Эйнштейн заметил, что она действительна "независимо от того, какими причинами обусловлено возникновение кривизны поверхности".
Можно понять восхищение, испытанное Эйнштейном, когда он ознакомился с логикой рассуждений и формулой Кельвина. Ведь, казалось бы, Кельвин обсуждал совсем частный пример: широкий сосуд, в нем жидкость, в жидкости капилляр и т. д. А пришел к закону природы огромной важности и выразил его формулой, в которой ничего не содержится от того частного примера, который обсуждался. Разве что только R - радиус тонкой трубочки. Но ведь трубочка, как оказалось, нужна была только для того, чтобы получить участок изогнутой поверхности, ограничивающей жидкость.
Вспомним о капле. Она вся ограничена изогнутой поверхностью, и, значит, давление пара вблизи нее будет повышено на величину, определяемую формулой Кельвина: чем меньше радиус капли, тем большее давление пара над ней. В этом легко убедиться с помощью многих опытов, далее мы с ними еще встретимся, а здесь, вместе с Эйнштейном, восхитимся талантом Кельвина - его проницательным умом и великолепной логикой.
Капля пустотыМного лет подряд вместе с моим ныне покойным учителем Борисом Яковлевичем Пинесом мы занимались изучением пористых кристаллических тел. Так случилось, что я ни разу не спросил, как у него возникло представление о капле пустоты - поре в кристалле. А сейчас, к сожалению, спросить уже некого и остается лишь строить догадки, сопоставляя факты и отрывки случайных разговоров.
Образ капли пустоты прочно вошел в физику твердого тела, о нем вспоминают всякий раз, когда надо осмыслить поведение различных дефектов в кристалле. И я расскажу о том, как этот образ возник. На примере рождения образа капли пустоты можно проследить, как вяжется логическое кружево мысли ученого, где сосуществуют и конкурируют фантазия и строгая формальная логика.
Борис Яковлевич не очень был склонен к аналогиям, упрощенным моделям, картинам, иллюстрирующим мысль. Он часто повторял, что картина - образование двумерное и, следовательно, неглубокое. Аналогия может появиться позже, а вначале должна быть формула, численная оценка. И еще, посмеиваясь, он любил говорить о том, что иных формулы гипнотизируют, поскольку формула - это математика, а математика, как известно, наука точная. Это преувеличенное почтение к формулам обычно испытывают люди, которые никогда не создавали их и поэтому не чувствуют ни их слабостей, ни таящихся в них возможностей.
Первая работа Бориса Яковлевича, посвященная изучению поведения пор в кристаллах (она появилась еще в 1946 г.), начинается с анализа давно известной формулы лорда Кельвина, которая устанавливает связь между давлением пара вблизи изогнутой поверхности капли (PR), ее радиусом (R) и давлением пара вблизи плоской поверхности жидкости, из которой капля состоит (Pо). Вот эта формула:
PR - Pо = (2a/R)(w/kT)Pо
В нее входят величины поверхностного натяжения (a), объема, приходящегося на один атом в жидкости (w), температуры (Т) и некоторая постоянная величина k, так называемая постоянная Больцмана.
Эта формула нам встречалась в предыдущем очерке о лорде Кельвине. Выглядела она там немного иначе, чем здесь: вместо множителя Pоw/kT стоял множитель ro/r. Можно убедиться, что эти множители равны друг другу. Действительно, отношение плотностей равно отношению числа частиц в единице объема: ro/r = no/n. Так как для газа no = Pо/kT, а для твердого тела или жидкости n = 1/w, то ro/r = Pоw/kT.
Легко заметить, что в формуле Кельвина нет ничего специфически "жидкого" и ее можно применять и к твердым закристаллизовавшимся каплям. Надо только при этом помнить, что поверхностное натяжение зависит от ориентации кристаллографических плоскостей, ограняющих застывшую каплю. Но это деталь, а в главном формула применима к твердым кристаллическим каплям. Из формулы следует, что чем меньше капля, т.е. чем меньше ее радиус, тем на большую величину давление пара вблизи ее поверхности превосходит давление пара вблизи плоской поверхности вещества, из которого капля состоит.
Понять это легко. Ведь что означают слова "упругость пара больше" или "упругость пара меньше"? Они означают, что при прочих равных условиях в газе вблизи поверхности будет большая или меньшая концентрация атомов вещества капли. Атом, который расположен на искривленной поверхности капли, имеет меньшее число соседей, чем тот, который расположен на плоской. В случае предельно маленькой капли, состоящей из одного атома, этот атом и находился бы на "поверхности" в единственном числе, вообще не имея соседей. Капля из одного атома, конечно же, никакая не капля, но эта условность помогает почувствовать тенденцию: чем меньше капля, тем меньше соседей у атома, сидящего на ее поверхности. А меньше соседей - меньше связей, удерживающих атом на поверхности, меньше связей - легче оторваться, легче оторваться - большее число атомов это совершит, и, следовательно, большая их концентрация будет в газе вблизи поверхности. Именно это строго описывает формула.
Борис Яковлевич прочел эту формулу по-своему, неожиданно и формально очень строго. Он обратил внимание на то, что она примечательна не только теми величинами, которые входят в нее, но и теми, которые в ней отсутствуют. Из величин, характеризующих вещество капли, в формулу входят лишь поверхностная энергия и объем, приходящийся на один атом. Масса атома не входит. Формально это означает, рассуждал он, что формула годится для вещества с любой массой атома, от бесконечной до равной нулю. Бесконечная масса - это по ту сторону разумного, а вот о "веществе" с нулевой массой "атома" можно говорить вполне серьезно, не забывая, однако, о кавычках. Таким "веществом" является пустота.
Несколько странное соседство слов "вещество" и "пустота". В действительности имеется в виду не "вещество", а отсутствие вещества. Например, в узле кристаллической решетки нет атома, которому следовало бы в этом узле быть. Этот свободный от атома узел можно назвать "атомом пустоты", а физики его иногда называют "вакансией". Очевидно, скопление большого количества "атомов пустоты" должно образовать "каплю пустоты", т.е. пору. Все это по аналогии с реальными атомами и реальным веществом: скопление большого количества, скажем, атомов железа, образует жидкую каплю железа. Разумеется, при температуре более высокой, чем температура плавления железа.
Итак, пустой узел в кристаллической решетке - "атом пустоты", пора в кристалле - "капля пустоты", и они должны подчиняться формуле, которая впервые была написана более 100 лет назад и применительно к "капле пустоты" впервые прочтена Борисом Яковлевичем Пинесом.
Теперь о следствиях нового прочтения формулы. И не обо всех, а о самом главном, ради которого стоило пристально всмотреться в старую формулу и заново ее прочесть.
Вот опыт, который демонстрируют на школьных уроках физики или рассказывают о нем. Небольшой стеклянный колпак (перевернутый стакан) установлен на стекле. Под колпаком блюдечко с водой и рядом на предметном стеклышке капли воды. Эти капли надо поместить на стеклышко после того, как пространство под колпаком насытится водяным паром, который образуется над плоской поверхностью воды в блюдце. Через некоторое время капли исчезнут: они испарятся, а возникшие при этом в водяном паре молекулы воды сконденсируются на поверхности воды в блюдце.
Рис. 7. Перенос жидкости из капли в блюдце Итак, в начале опыта под колпаком было три объекта: вода в блюдце, вода в каплях и насыщенный водяной пар. Опыт окончился, когда один из объектов исчез - капель не стало. Здесь все ясно: согласно формуле, давление пара над изогнутой поверхностью водяной капли больше, чем над плоской поверхностью воды в блюдце, и пар под влиянием этой разности давлений двигался по направлению к блюдцу - уходил оттуда, где его давление больше, и приходил туда, где его давление меньше. Чтобы вблизи своей поверхности поддерживать давление, предписываемое ей формулой, капля должна все время испаряться. Она это добросовестно делала и в конце концов исчезла.
А теперь тот же опыт, только не с каплями и атомами реальной жидкости, а с "каплями" и "атомами" пустоты. Вместо колпака с блюдцем и каплей - монокристалл. Он огранен плоскими поверхностями и в объеме имеет одну пору сферической формы. Вблизи изогнутой поверхности поры (капли!) концентрация вакансий повышена, а вблизи плоской поверхности, которая отделяет кристалл от окружающего пространства (вода в блюдце!), концентрация вакансий нормальная, не повышена. Очевидно, появится поток вакансий от поры к поверхности кристалла, и, подобно капле воды, пора исчезнет - "испарится в кристалл". Образовавшийся при этом в кристалле избыток вакансий со временем сгладится: вакансии либо поглотятся внутренними стоками, либо с помощью диффузии переместятся к внешней поверхности кристалла.

Рис. 8. Капля пустоты (пора) испаряется в кристалл.
Вблизи поры много вакансий (зачерненные кружки), вдали - малоНачали мы опыт с пористым, а окончили с беспористым кристаллом! Как быстро это произойдет? Все зависит от размеров поры и температуры кристалла. Например, пора, радиус которой один микрон, в медном кристалле при температуре 1000° С исчезает приблизительно за 30 мин.
Все рассказанное о формуле, об аналогии между реальными каплями и каплями пустоты лежит в основе целого раздела современной физики твердого тела - физики спекания, которая объясняет, как пористые кристаллические тела самопроизвольно при высоких температурах превращаются в плотные. Оказывается, капли пустоты могут испаряться в кристалл!
Удобная "постель" для каплиВ названии очерка нет надуманности: его содержание находится в полном соответствии с названием. Дело в том, что гладкая, чистая, полированная поверхность твердого тела для жидкой капли неудобна. Попав на нее, капля будет пытаться изменить, улучшить подложку, сделать ее более удобной, даже если для этого ей придется трудиться очень долго.
Напомню, что нет ничего удобнее для капли, чем быть взвешенной в пространстве, в невесомости: ни с чем она не соприкасается, никакие силы ее не искажают и ни к каким изменениям она не стремится. А на пластинке с плоской поверхностью все не так, даже если пластинка с каплей находится в невесомости.
Вначале подумаем над тем, чем гладкая поверхность неудобна для жидкой капли. Казалось бы, капля подвижна и должна, переливаясь, как-то приспособиться к плоской поверхности, сделать свое пребывание на ней удобным. Оказывается, что одним изменением собственной формы добиться этого капля не может.
Посмотрите на приведенный рисунок. На нем изображена капля жидкости, смачивающей твердую поверхность (угол j - острый). Стрелками обозначены силы, обусловленные поверхностным натяжением на границе подложка - капля (a21), подложка - воздух (a20) и капля - воздух (a10). Все дальнейшее можно было бы рассказать, имея в виду и каплю, не смачивающую твердую поверхность. Но мы остановимся на случае, который изображен на рисунке. Из него с очевидностью следует, что три силы, которые соответствуют поверхностным натяжениям твердое - воздух, твердое - капля и капля - воздух, ни при какой форме капли не могут прийти в равновесие, так как первые две из них направлены одна против другой и лежат в одной плоскости, а третья - под углом к ней. Именно поэтому имеется нескомпенсированная сила, приложенная к контуру капли, на рисунке она обозначена жирной стрелкой и, пожалуй, может считаться количественной мерой степени неудобства подложки. Капле надо сделать что-либо с собой или с подложкой, чтобы избавиться от этой силы.Риc. 9. Взаимное расположение сил, действующих на контур капли,
лежащей на гладкой твердой поверхности
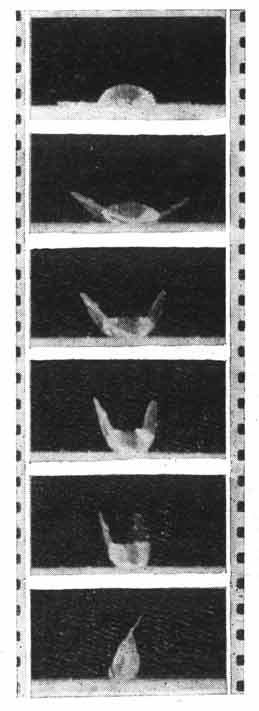
Рис. 10. Водяная капля заворачивается
в тонкую полимерную пленкуМожно рассказать об этом по-другому. Выпуклая поверхность капли создает давление, которое прижимает ее к плоскости. Это так называемое капиллярное (лапласовское) давление, мы уже с ним встречались. Участок же поверхности капли, который граничит с твердой подложкой, такого давления не создает: оно должно быть пропорциональным 1/R, а радиус кривизны плоского участка поверхности капли равен бесконечности, и, значит, давление равно нулю. К одному участку поверхности давление приложено, к другому - не приложено, а это неудобно. Капля, подвешенная в невесомости, таких неудобств не испытывает. Она вся подвержена равномерному давлению всестороннего сжатия. Два разных рассказа об одном и том же явлении можно проиллюстрировать двумя опытами. Опыт первый иллюстрирует первый рассказ, опыт второй - второй.
Опыт первый. На полированной поверхности стеклянной пластинки, сухой и чистой, располагается тонкий лепесток полимерной пленки. Хорошо, если его толщина будет не более 5 микрон. На поверхность лепестка надо посадить каплю воды и наблюдать за происходящим. Капля начнет изгибать пленку, стремясь завернуться в нее. Отчетливо это иллюстрирует приводимая кинограмма. Работает при этом та сила, которая на рисунке обозначена жирной стрелкой. Если бы полимерная пленка абсолютно подчинялась воле капли, произошло бы следующее: капля приняла бы форму сферы, равномерно покрыв себя слоем полимерной пленки. В действительности же, так как плоская пленка не может приобрести сферическую форму, капле не удается полностью в нее завернуться, но все же устраивается она при этом удобнее, чем на плоской поверхности.
Стремление капли завернуться в пленку мы объяснили, сославшись на силу, изображенную жирной стрелкой. Можно и в иных словах и понятиях описать процесс, запечатленный на кинограмме, смонтированной из кадров фильма, в котором заснята кинетика заворачивания водяной капли в пленку.
Первый кадр кинограммы свидетельствует, что капля воды смачивает полимерную пленку и располагается на ней так, как схематически изображено на предыдущем рисунке со стрелками.
Из рисунка 9 следует, что a21 + a10cosj = a20. Так как cosj > 0, то a21 < a20 и, следовательно, заведомо меньше, чем сумма a20 + a10. Это означает, что выгодно вместо двух свободных поверхностей капли и пленки создать одну поверхность, вдоль которой капля и пленка соприкасаются. А для этого капле следует в пленку завернуться, что она и делает.
Внимательно присмотритесь к каплям, которые после дождя остались на поверхности тонких листиков, и увидите, что вблизи капель листики изогнуты значительно больше, чем это могло бы произойти лишь под влиянием их веса. Капли явно готовили себе "постель" поудобнее.
Опыт второй был поставлен чешскими физиками. На полированную поверхность массивного кристалла железа наносилась капля расплавленного свинца. Железо было раскалено до температуры более 1000° С, и поэтому свинцовая капля оставалась жидкой. Кристалл железа - не полимерная пленка, и изогнуть его вокруг себя капля не может. Поэтому поступает она иным способом: выкапывает под собой ямку такой формы, чтобы вдоль контуров капли все три силы скомпенсировались так, как показано на рисунке. Эта "удобная" ямка должна иметь такую форму, чтобы давление, обусловленное изогнутой поверхностью жидкий свинец - воздух, было в точности равно тому давлению, которое обусловлено искривленностью поверхности жидкий свинец - твердое железо, т.е. дна ямки. Равенство этих давлений означает, что a10/R10 = a12/R12. Итак, давления равны, а кривизна двух поверхностей различна, потому что различны соответствующие поверхностные энергии. Выкопав под собой ямку, капля как бы перенеслась в невесомость: как и в невесомости, капиллярное давление оказалось одинаковым вдоль всей поверхности, ограничивающей каплю.
Естественно возникает вопрос: каким образом капля выкопала ямку? Ответим на него. Вначале, когда капля была расположена на плоской поверхности железа, она прижималась к нему тем давлением, которое обусловлено искривленностью поверхности свинец - воздух. Под влиянием этого давления железо из-под свинцовой капли перемещалось в области вокруг нее. Перемещалось в процессе диффузии поатомно, атом за атомом - опыт ставился при высокой температуре, когда диффузия в железе происходит достаточно активно.
Надо подчеркнуть, что в описанном опыте капиллярное давление, которое обусловливает перемещение железа из-под свинцовой капли, существенно больше давления, обусловленного ее весом, так как капля свинца была очень "маленькая" в том смысле, в каком мы об этом говорили в очерке об опыте Плато.Рис. 11. Взаимное расположение сил, действующих на контур капли, которая "удобно устроилась" на твердой поверхностиИтак, в названии очерка все точно. Попав на твердую поверхность, капля действительно готовит себе удобную постель: либо изгибает подложку, если ей это удается, либо выкапывает для себя удобную ямку.
Раздавленная капляАналогия рождается на перекрестках памяти и раздумий и иногда связывает воедино образы и события, состоящие в очень дальнем родстве. Неожиданная аналогия, даже отдаленная или поверхностная, родившись вовремя, может помочь исследователю выйти из тупика и осветить путь к решению.
Когда-то, в конце 40-х годов, я участвовал в коллективной экспериментальной работе. Ее цель заключалась в определении физических характеристик вещества, которое ранее не исследовалось. Ранее этого вещества в чистом виде просто не было: ценой больших усилий его получили химики.
На первый взгляд задача совсем не новая, и решать ее следует, двигаясь путями, проторенными многими исследователями, изучавшими физические характеристики других веществ. Наша задача, однако, была усложнена тем, что экспериментировать мы могли лишь с микроскопическими крупинками. Каждая крупинка весила около одной миллионной грамма, а размер ее - несколько десятков микрон. Число крупинок было ограниченно: химики их добывали с трудом.
Группа, в которой я работал, должна была определить температуру плавления и поверхностное натяжение вещества в жидкой фазе.
В обычном "макроскопическом" эксперименте температура плавления измеряется просто: в образец погружают термометр и следят за тем, как меняются его показания по мере нагрева образца. Температура постепенно возрастает. Когда она достигнет некоторого значения, ее рост приостановится в связи с тем, что тепло, притекающее к образцу, начнет расходоваться не на нагрев, а на процесс расплавления. Эта температура и является температурой плавления. Когда же масса крупинки - одна миллионная грамма, термометр внедрить в нее невозможно и для определения температуры плавления следует искать обходные пути.
Один из участников нашей группы, у которого за плечами были годы работы в литейном цехе, предложил совсем неожиданное решение задачи. Его память хранила воспоминание, родившее аналогию. В годы войны, сказал он, я вел плавку одновременно в нескольких одинаковых тигельных электропечах. Загружал их алюминиевыми чушками и, чтобы определить начало расплавления шихты в печи, не забираясь на ее загрузочную площадку, в каждую печь между чушками вертикально устанавливал длинный металлический стержень, который был виден над печью. В момент начала плавления стержень наклонялся - это служило сигналом.
Воспоминание подсказало идею, с помощью которой можно было измерить температуру плавления крупинки. Опыт заключался в следующем. На тщательно отполированной пластинке кварца располагалась крупинка. Сверху ее накрывали другой пластинкой кварца, которая, касаясь крупинки, образовывала некоторый угол с первой пластинкой. Это устройство нагревали, и в момент, когда крупинка расплавлялась, верхняя пластинка раздавливала образовавшуюся каплю и угол между пластинками скачкообразно уменьшался. Чтобы надежнее этот момент зарегистрировать, на внешнюю поверхность верхней пластинки нанесли зеркальное покрытие и следили за тем, как отражаемый от нее луч скачком смещается. Пластинка, меняющая свое положение, была подобна металлическому стержню, который наклонялся, свидетельствуя о начале процесса плавления. Так как масса крупинки пренебрежимо мала по сравнению с массой кварцевых пластинок, между которыми она зажата, температура крупинки равна температуре пластинок и, следовательно, измерить ее совсем просто.
В описанном опыте, вопреки известной пословице, нам удалось поймать двух зайцев: определить, во-первых, температуру плавления и, во-вторых, величину поверхностного натяжения расплавленного вещества. Дело в том, что верхняя пластинка, раздавливая своей тяжестью каплю, превращала ее в лепешку определенной толщины. Сколько раз ни повторялся бы опыт по расплавлению одной и той же крупинки, образовывавшаяся жидкая капля весом пластинки расплющивалась до одной и той же толщины h. Эту величину можно было уменьшить, увеличивая вес верхней пластинки. Легко понять, что дальнейшему расплющиванию препятствуют силы поверхностного натяжения, приложенные к той части поверхности расплющенной капли, которая граничит с воздухом. В наших опытах вещество капли практически не смачивало кварц (именно поэтому опыты и ставились с кварцевыми пластинками) и, следовательно, можно считать, что радиус закругления свободной поверхности r = h/2.
Величина поверхностного натяжения a может быть определена из условия равенства давления, которое оказывает пластинка на жидкую каплю (Рп), и лапласовского давления (Рp), которое обусловлено искривленностью ее свободной поверхности. Если вес пластинки давит на каплю с силой F, а площадь ее контакта с расплющенной каплей pR2, то Рп = F/pR2. Величина Рp = a/r = 2a/h. Приравнивая Рп к Рp, находим формулу, с помощью которой можно определить величину поверхностного натяжения вещества:
a = Fh/2pR2
Величины h и R можно измерить с большой точностью, а силу F легко определить, зная вес верхней пластинки. Способ решения стоящей перед нами задачи, который подсказала возникшая вдруг аналогия, конечно, был не единственно возможным. Видимо, можно было придумать и иные приемы, но нас привлекли в нем неожиданность аналогии и возможность опровергнуть пословицу о двух зайцах.
| Оглавление | Естествознание | VIVOS VOCO! |