№9, 2003 г.
© В.И.Найденов, И.А.Кожевникова
Почему так часто
происходят наводнения?В.И. Найденов, И.А. Кожевникова
Вячеслав Иосифович Найденов, д.ф.-м.н., зав. лаб. поверхностных вод Института водных проблем РАН.
Ирина Аркадьевна Кожевникова, к.ф.-м.н.,, вед. научн. сотр. мехмата МГУ.Истинные законы не могут быть линейными…
А.Эйнштейн
В России катастрофы происходят все чаще, особенно в последние годы [1]. Катастрофические явления, вызванные наводнениями, составляют 19% от общего числа. Наводнения занимают первое место в ряду стихийных бедствий по повторяемости, охвату территории и материальному ущербу. Ежегодно по стране затопляются обширные территории (в среднем около 50 тыс. км2), на которых находятся больше 300 городов, десятки тысяч других населенных пунктов, множество хозяйственных объектов, сельскохозяйственные угодья (40% затапливаемых площадей).
Самое масштабное и разрушительное за 100 лет наводнение на Северном Кавказе потрясло Россию в прошлом году. Общая площадь затопления составила 346 км2, были эвакуированы более 100 тыс. человек, 104 человека погибли. Материальный ущерб от стихийного бедствия - почти 14 млрд руб. Версий случившегося много…
С точки зрения статистики
Гидрологи предполагают, что катастрофические наводнения происходят как “следствие необычного сочетания гидрометеорологических факторов и условий на водосборе” [2]. Но если бы это было так и к наводнениям приводило бы суммарное действие множества не поддающихся учету факторов (количество дождей, их интенсивность, тепло- и влагообмен атмосферы с поверхностью), то, согласно центральной предельной теореме теории вероятностей, величина уровня воды в реках принимала бы значения в соответствии с гауссовским распределением. Тогда, действительно, вероятность катастрофы на Северном Кавказе была бы ничтожно мала, и можно было бы считать, что нам сильно не повезло.
Однако при внимательном анализе статистических данных по крупнейшим наводнениям выясняется, что налицо весьма необычные особенности, не укладывающиеся в привычные представления. Так, при наводнении 1931 г. на р. Янцзы в Китае погибло около 1.3 млн человек, что в десятки тысяч раз превосходит число погибших при рядовом наводнении в тех же местах. Во временнОм ряду величин ущерба от катастроф изредка встречаются экстремальные значения, несоизмеримые со значениями для подавляющей части событий. Не составляет исключение и наводнение на Северном Кавказе: материальный ущерб от него гораздо выше, чем общий ущерб за десятки предыдущих наводнений.
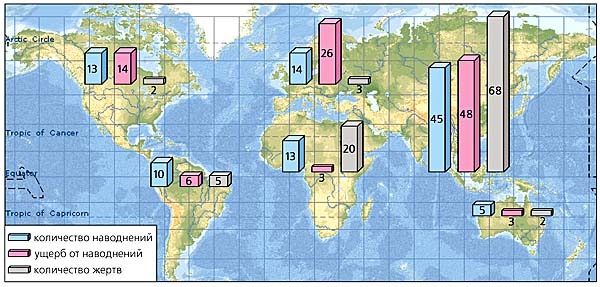
Карта-диаграмма распределения по частям света числа наводнений, жертв и размеров ущерба от них
(в % от мировых величин за период 1998-2002 гг. - указаны цифрами).Как известно математикам [3], временнoй ряд, обладающий указанным свойством (сумма элементов ряда имеет тот же порядок, что и максимальный элемент ряда), должен подчиняться распределению Парето, которое характеризуется медленным уменьшением числа редких событий - степенному распределению с “тяжелым хвостом”. Для такого распределения вероятность катастрофических наводнений на порядок и больше превышает вероятности, вычисленные на основании экспоненциального семейства распределений.
Карта района наибольших наводнений 2002 г. в восточной части Предкавказья (область затопления обозначена голубым). И в самом деле, американская статистика торнадо, землетрясений, наводнений, ураганов за прошедший век показывает, что данные наблюдений с достаточно хорошей точностью подчиняются степенной статистике [4, 5]. Разница между нормальным и степенным распределениями носит не формальный, а принципиальный характер. Если статистика случайной величины описывается гауссовским законом, то в более чем 99.7% событиях величина отклоняется от среднего значения менее чем на 3s (s - стандартное отклонение), а, скажем, за границу 5s выбивается и вовсе реже чем в одном случае из миллиона. Поэтому очень “крупными” событиями, когда случайная величина достигает значений много бОльших среднего, можно пренебречь, считая их практически невероятными. Примерно такие соотношения имеют место для любого распределения из экспоненциального семейства. Статистика, описываемая степенными распределениями, отличается тем, что “крупные” события, приходящиеся на “хвост” распределения, происходят не настолько редко, чтобы их можно было не учитывать. Именно с этой ситуацией мы сталкиваемся при оценке вероятностей катастрофических наводнений. Если использовать для стандартной обработки временнЫх гидрологических рядов распределение из семейства экспоненциальных, как рекомендуют Строительные нормы и правила (СНИП 2-01.14-83), очевидно, что катастрофические наводнения будут для нас всегда неожиданными. Наводнения исключительной силы последних лет убедительно показали, что рассчитывать защитные дамбы, плотины и другие гидротехнические сооружения необходимо на основании иных вероятностных закономерностей.
Например, в Нидерландах к началу 20-х годов прошлого века правительственный комитет по защите от наводнений установил уровень защитных сооружений в 390 см - такой подъем воды на побережье никогда не наблюдался. Гидротехники не стали ориентироваться на столь редкое событие и приняли величину 340 см с вероятностью достижения этого уровня раз в 70 лет. Это значение было всего на 12 см выше абсолютного максимума, зарегистрированного для периода примерно в 25 лет. Стремление удешевить строительство обернулось трагедией 1 февраля 1953 г., когда ураган унес около 2000 жизней и вызвал огромные разрушения. Ныне в Нидерландах гидротехнические сооружения решено строить в расчете на максимальный уровень 500 см, возможный лишь раз в 10 000 лет.
Гидрология пока не способна объяснить физический механизм возникновения распределения Парето и тем самым ответить на фундаментальный вопрос: почему катастрофические наводнения происходят так часто?
С точки зрения описания случайных процессов это означает, что распределения вероятностей случайных величин, характеризующих наводнения (уровни воды в реке, объемы стока за половодье, максимальные расходы воды и т. п.), являются “распределениями с тяжелыми хвостами”. В терминах оценки безопасности и риска “хвост” распределения соответствует так называемым гипотетическим наводнениям, возможность которых на практике пока не учитывается. Наличие степенного закона распределения вероятностей в корне изменяет наши представления о возможных масштабах наводнений.
Этот универсальный степенной закон
Степенное распределение вероятностей совсем не экзотика: оно характерно и для многих других катастрофических событий. Пусть N - число бедствий, в которых число погибших больше некоторой величины х. Хорошо известно, что величина N при x>>1 имеет вид
(1)
где показатель a обычно лежит в диапазоне от 0 до 2. При статистическом описании катастроф и стихийных бедствий это распределение оказывается правилом, практически не знающим исключений. Так распределены последствия следующих бедствий: наводнений (a ~1.35), торнадо (a ~ 1.39), ураганов (a ~0.58), землетрясений (a ~ 0.41) [6]. Степенное распределение имеют характеристики и многих других явлений: эпидемий, лесных пожаров, снежных лавин, солнечных вспышек, столкновений метеоритов с Землей.
Покажем, как подобные распределения могут возникнуть в гидрологических процессах. Рассмотрим водный баланс речного бассейна. Изменение его влагозапаса (объема воды) W вызвано поступлениями за счет осадков Р и расходом за счет испарения Е, а также речного стока Q:
здесь P и E - средние многолетние величины осадков и испарения, x(t) - гауссовский случайный процесс, учитывающий их колебания, s2 - его дисперсия.
Однако не все величины, входящие в это уравнение, независимы: величина влагозапаса влияет на сток, причем есть основания полагать, что зависимость Q = Q(W) - нелинейная.
Физический механизм увеличения стока с ростом влагозапасов заключается в следующем. Во-первых, чем больше объем поверхностных, почвенных, подземных вод, вод озер и болот, составляющих влагозапасы бассейна, тем выше потенциальная энергия этих вод. Во-вторых, величина диссипации энергии при движении воды в увлажненном бассейне гораздо меньше, чем в “сухом” (именно по этой причине коэффициент фильтрации воды резко увеличивается с ростом влажности почвы, а влажной тряпкой гораздо легче вытереть лужу). Увеличение потенциальной энергии воды и уменьшение сопротивления ее движению в совокупности ведут к нелинейному увеличению расхода.
Из теории случайных процессов известно [7], что уравнению (2) можно поставить в соответствие другое - уравнение Фоккера-Планка-Колмогорова для плотности вероятностей величины Q.
Можно показать: стационарное решение этого уравнения в случае нелинейной зависимости стока от влагозапасов имеет степенную асимптотику в области больших значений Q. Следовательно, нелинейная динамика речного стока и случайность внешней среды (климатический шум) при определенных условиях приводит к появлению компоненты Парето в распределении плотности вероятности величины Q.
Физически появление степенного закона объясняется тем, что два важнейших фактора - увеличение влагозапасов и уменьшение сопротивления движению воды в бассейне - оказываются зависимыми, и случайный процесс колебаний стока уже не может быть гауссовским. Допустим, что в бассейне реки прошли обильные дожди; в этом случае сопротивление движению воды настолько уменьшится, что в реку попадут не только выпавшие осадки, но и осадки от предыдущих дождей, которые ранее из-за большого сопротивления трения не могли проникнуть в реку. Подчеркнем: само выпадение осадков следует гауссовскому закону, а “тяжелый хвост” распределения формируется гидрофизическими процессами на водосборе, и важно то обстоятельство, что в формировании стока в данный момент участвуют осадки предыдущих времен. Математическая формализация этого известного гидрологического явления и дает в итоге степенные законы вероятностей паводков и наводнений.
Например, ранней весной 1997 г. Северные равнины (Средний Запад США) были накрыты опустошающим наводнением. Города, стоящие на Ред-Ривере, такие как Гранд-Форкс и Северная Дакота, оказались полностью затопленными и парализованными. А в предыдущем году, во время ливней, города на Ред-Ривере получили рекордное количество осадков. Зимой вода замерзла прежде, чем успела стечь в океан. В течение долгой зимы выпало опять-таки рекордное количество снега, а когда началось потепление, этот снег начал таять. Однако таять начал не только он, но и замерзшая дождевая вода, оставшаяся от предшествующего сезона дождей. В результате высвободилось много воды, которая не могла локализоваться в ручьях и реках, и оказались затопленными огромные участки суши.
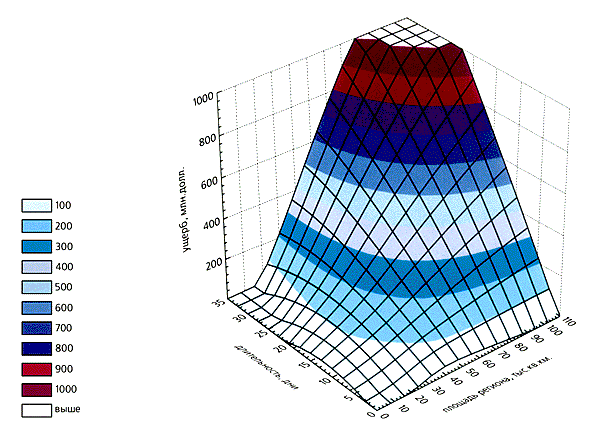
Ущерб от наводнений в США (2002 г.) в зависимости от их длительности и площади затопления.
Рассмотренный выше механизм характеризует речные наводнения; морской механизм наводнений, как на Неве, конечно же, другой, но тоже нелинейный, описываемый нелинейными уравнениями движения воды в Финском заливе. Как хорошо известно, даже малые нелинейности в динамической системе существенно изменяют именно “хвосты” распределений и, следовательно, оценки вероятностей катастроф.
Следим за уровнем воды
Мы провели статистический анализ множества временнЫх рядов максимальных уровней воды в реках, объемов стока за половодье, максимальных расходов воды. Особое внимание уделялось катастрофическим наводнениям в Санкт-Петербурге, так как для этого явления разработаны детальные физические модели и есть хорошая возможность сравнить вероятностные и гидродинамические методы расчета.
Рассмотрим два распределения, одно из которых хорошо известное гамма-распределение
а другое,
при больших х асимптотически переходит в степенное (т. е. дает степенной “хвост” x–b). Здесь m>0, b>2 - параметры распределений, G - гамма-функция Эйлера.
В теории вероятностей это распределение известно как распределение Пирсона пятого типа, и оно является решением уравнения Фоккера-Планка-Колмогорова для (2) при определенных нелинейных зависимостях стока от влагозапасов. Использовать его в гидрологии мы предложили впервые [8, 9].
С точки зрения математики, отличительная черта распределения (3) - отсутствие моментов [b]-го порядка ([b] - целая часть b), что качественно отличает степенное распределение от семейства экспоненциальных распределений, для которого существуют все моменты. Например, при 2<b<3 это распределение имеет бесконечную дисперсию.
Когда случайный процесс, имеющий степенной закон распределения (3), реализуется во времени, периодически возникают заметные отклонения величины от среднего, причем гигантские выбросы особенно часто встречаются при малых значениях b.
Мы оценили параметр b для десятков гидрологических рядов максимальных уровней (расходов воды). Например, для максимальных уровней воды в Неве (1878-1994) было получено b=16.28. Для этого были построены функции распределения вероятностей максимальных уровней воды у Горного института. Вероятности превышения уровня, вычисленные на основании данного распределения, приведены в [8, 10].
На основе анализа различных критериев согласия можно утверждать, что и гамма-распределение, и степенное распределение удовлетворительно соответствуют натурным данным [9]. Однако вероятности катастрофических наводнений, вычисленные на основе этих распределений, существенно различаются.
Например, такое наводнение, как знаменитое наводнение в Санкт-Петербурге, произошедшее 19 ноября 1824 г. (уровень воды в Неве на 421 см выше ординара), должно происходить один раз в 667 лет с точки зрения степенного распределения. По гамма-распределению это событие практически невозможно (происходит реже чем один раз в 20 000 лет). Наводнение, случившееся 23 сентября 1924 г. (уровень воды в Неве 380 см), имеет вероятность 0.0039 (раз в 256 лет) по степенному распределению и 0.00036 (раз почти в 3000 лет) по гамма-распределению, т. е. снова малореально. Но оба эти события имели место.
В связи с гидрологическим обоснованием ряда проектов защиты Санкт-Петербурга и ближайших пригородов от наводнений были проведены обширные научные исследования по проблеме расчета максимальных уровней воды на Неве [11-14].
Мы сравнили результаты этих исследований (второй столбец в таблице) с расчетами по статистическим моделям (третий и четвертый столбцы). Это сравнение показывает, что степенное распределение лучше соответствует гидродинамическим моделям наводнений.
Реализации степенного закона (3) при различных параметрах: а) b=5, б) b = 7, в) b = 15, г) b = 25.
Подчеркнем, что для вычисления вероятностей превышения уровней, приведенных в таблице, использовались статистические данные по максимальным уровням воды в Неве только за период 1878-1994 гг. Оказалось, что статистика петербургских наводнений за весь период 1703-1994 гг. хорошо описывается тем же степенным законом, параметры которого удалось найти по относительно короткому ряду наблюдений.
Отмеченная закономерность характерна и для других рек.
Наводнение 1954 г. на р.Янцзы в Китае имеет вероятность в четыре раза бОльшую по степенному распределению (повторяемость один раз в 167 лет), чем по гамма-распределению (раз в 667 лет). Вероятность превышения максимального расхода воды на р.Миссури в 1951 г. (12606 м3/с) по степенному распределению равна 0.026 (раз в 38 лет), а по гамма-распределению 0.0055 (раз в 181 год), т. е. в пять раз меньше.
Другой пример. Вероятность превышения катастрофического уровня половодья 1931 г. на р. Западная Двина у Витебска по степенному распределению равна 0.0114 (раз в 88 лет) и превышает вероятность по гамма-распределению, составлющую 0.0019 (раз в 526 лет), в шесть раз. Подчеркнем, что в 1951 г. катастрофический подъем уровня воды на Западной Двине повторился.
Летом 2002 г. на реках Северного Кавказа (Кубани, Тереке, Куме, Подкумке и т. д.) наблюдался аномальный гидрологический режим. Расчеты, выполненные на основе разных распределений максимальных расходов воды, показали следующее. Максимальный расход воды на Кубани может превысить среднемноголетний в два с половиной раза единожды в 170 лет по степенному распределению и в 1000 лет по гамма-распределению. Терек может удвоить свой расход по отношению к обычному один раз в 110 лет по степенному распределению (один раз в 406 лет по гамма-распределению). Для Кумы сток воды, превышающий норму в пять раз, может произойти по степенному распределению один раз в 85 лет (по гамма-распределению - один раз в 28 000 лет). В Подкумке расход воды, который выше нормального в четыре раза, может случиться один раз в 102 года по степенному распределению (один раз в 8800 лет по гамма-распределению). Аналогичные оценки верны и для других больших и малых рек Северного Кавказа.
Другими словами, произошедшее здесь катастрофическое наводнение не является почти невероятным событием, а имеет достаточно большую вероятность повториться даже при жизни нынешнего поколения. Мы считаем, что подобные распределения вероятностей необходимо учитывать при сооружении новых защитных дамб, плотин и берегоукрепительных сооружений.
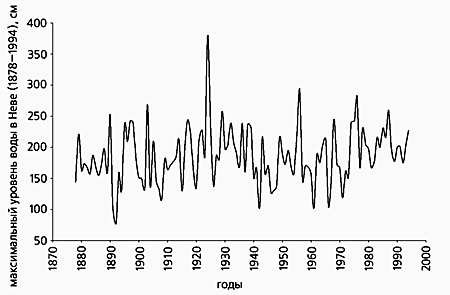
Максимальные уровни Невы у Горного института (1878-1994).
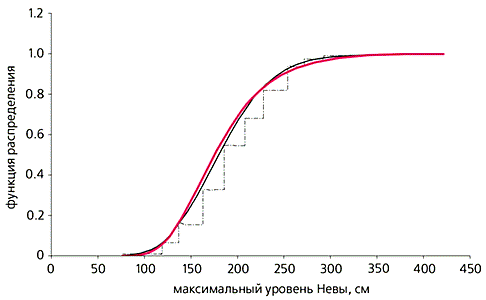
Функции степенного (цветная линия) и гамма- распределений и выборочная функция распределения,
построенная по натурным данным (ломаная линия) уровня воды в Неве.
Плотности степенного (цветная кривая) и гамма-распределений для максимальных уровней на Неве. На врезке показано поведение “хвостов” степенного (цветная линия) и гамма-распределений в области катастрофических наводнений.Разрушительным наводнением были охвачены летом прошлого года большие части Чехии и Германии. Мы проанализировали месячные стоки Эльбы в районе г.Дечина с 1888 по 1990 г. за июль-август и получили такие результаты. Августовский расход воды в Эльбе может превысить средний многолетний в 2.3 раза единожды в 35 лет по степенному закону и в 100 лет по гамма-распределению. Подобная закономерность верна и для июльских расходов (вероятность превышения нормы в три раза единожды в 100 лет по степенному закону и один раз в 1000 лет по гамма-распределению).
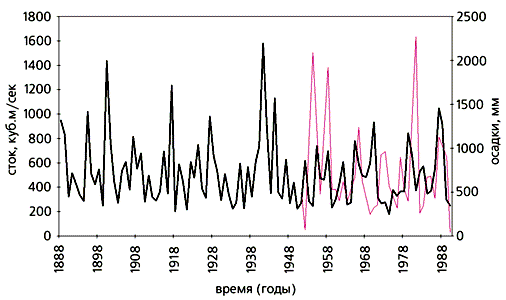
Июльский сток Эльбы у Дечина и осадки (цветная линия) в Праге.
Неизбежные потери
Оценки величины b, полученные нами для максимальных расходов воды и уровней, изменяются в широких пределах от 2.83 (Тура) до 27.56 (Янцзы) [8, 10], причем для больших рек эта величина значительно больше двух. Однако для величин ущерба (количество жертв, экономические потери) действует степенной закон с параметром a<2. Почему значение этой величины так мало? Примечательно, что для этого распределения отсутствуют математическое ожидание и дисперсия (соответствующие интегралы расходятся) и характерен эффект нелинейного роста ожидаемого ущерба со временем [9], т. е. сила наводнения может неограниченно возрастать. Один из авторов монографии [6] считает:
“Что касается физически или экономически обоснованных пределов возможной силы катастроф, то единственно несомненные из них связаны с ограниченностью размеров нашей планеты. Такие ограничения, однако, не конструктивны, так как соответствующие им события аналогичны по своим последствиям глобальной катастрофе - «концу света»”.Тем не менее рассмотренный выше физический механизм возникновения степенного закона позволяет предложить конструктивную гипотезу, ограничивающую физические размеры наводнений в исторических масштабах. Ясно, что в области больших увлажненностей речных бассейнов зависимость величины стока от влагозапасов значительно ослабевает (сколько осадков выпало, столько и стекает воды) и плотность вероятности очень больших величин стока в этом случае следует гауссовскому закону. Но так как в нашу климатическую эру увлажненность суши еще не велика, то степенной закон был справедлив для палеонаводнений и останется справедливым некоторое время и для грядущих катастроф.Небольшая же величина a<2 для значений ущерба от наводнений, полученная статистическими методами в работе [9], объясняется следующим образом. Если ввести новую случайную величину, например ущерб от наводнений, то разумно предположить, что этот ущерб будет нелинейно зависеть от физических масштабов бедствия (уровня или расхода воды). Из теории вероятностей хорошо известно, что плотность распределения этой величины будет иметь гораздо более “тяжелый хвост”, чем плотность распределения максимального уровня или расхода воды, что и объясняет степенной характер гистограмм распределений числа жертв и лишившихся крова из-за наводнений последних десятилетий ушедшего века.
Пусть Y = Xm, где Y - случайная величина, характеризующая ущерб, а X - случайная величина, характеризующая максимальный уровень реки (или максимальный расход) и распределенная в соответствии с (3). Тогда логарифм плотности распределения ущерба при больших Y имеет вид ln p(Y) ~ ((b–1)m–1 + 1)lnY. Статистические оценки показывают, что (b–1)m–1 = 0.84 [9].
Таким образом, степенная статистика констатирует: катастрофические наводнения, происходящие на нашей планете, не являются из ряда вон выходящими событиями, а имеют достаточно большую вероятность, и с этой вероятностью необходимо считаться. Хотя предложенная здесь модель достаточно проста, она открывает перспективу дальнейшего изучения процессов, ибо, как справедливо заметили авторы статьи [15]:
“Понимание редко возникает из сложного беспорядочного моделирования, а много чаще - из-за грубого упрощенчества. Как только определен существенный механизм, просто проверить его на прочность путем добавления все новых и новых деталей”.Работа выполнена при поддержке Российского фонда фундаментальных исследований. Проект 02-05-64123.
Литература
1. Осипов В.И. // Вестн. РАН. 2001. Т.71. №4. С.291-302.
2. Кучмент Л.С. Развитие физико-математических моделей гидрологического цикла суши// Воды суши: пробл. и решения. ИВП РАН. М., 1994. С.10-20.
3. Феллер В. Введение в теорию вероятностей и ее приложения. Т.2. М., 1967.
4. Embrechts P., Kluppelberg C., Mikossch T. Modeling extreme events for insurance and finance. Berlin, 1997.
5. Малинецкий Г.Г., Курдюмов С.П. // Вестн. РАН. 2001. Т.71. №3. С.210-232.
6. Управление риском: Риск. Устойчивое развитие. Синергетика / Под ред. акад.И.М.Макарова. М., 2000.
7. Хорстемке В., Лефевр Р. Индуцированные шумом переходы. М., 1987.
8. Найденов В.И., Кожевникова И.А. // Докл. РАН. 2002. Т.386. №3. С.338-344.
9. Кузнецов И.В., Писаренко В.Ф., Родкин М.В. // Экономика и математические методы. 1997. Т.33. Вып.4. С.39-50.
10. Найденов В.И., Кожевникова И.А. Российская наука: дорога жизни. М., 2002.
11. Goodness-of-fit techniques / Eds R.B.D’Agostino, M.A.Stephens. N.Y.; Basel, 1986.
12. Нежиховский Р.А. Вопросы гидрологии реки Невы и Невской губы. Л., 1988.
13. Померанец К.С. Наводнения в устье Невы // Природа. 1993. №10. С.9-19.
14. Померанец К.С. // Метеорология и гидрология. 1999. №8. С.105-109.
15. Bak P., Tang C., Wiesenfeild K. // Phys. Rev. A. 1988. V.38. №1. P.364-374.