є7, 2006 г.
© ћейлихов ≈.«.“рагическа€ и счастлива€ жизнь Ёрнста »зинга ≈.«. ћейлихов
≈вгений «алманович ћейлихов, доктор физико-математических наук,
главный научный сотрудник »нститута молекул€рной физики –оссийского научного центра У урчатовский институтФ.ћодель »зинга - одна из стандартных моделей статистической физики, исследованию которой посв€щено огромное число публикаций: известна€ интернетовска€ поискова€ система Google по запросу Умодель »зингаФ выдает 330 тыс. ссылок (!). ѕарадокс состоит в том, что хот€ многие слышали о модели »зинга, но почти никто не знает, кто такой »зинг. ћежду тем, Ёрнст (или Ёрнест) »зинг - автор работы, в которой впервые рассматривалась модель, названна€ позже его именем, и котора€ стала его первой и единственной публикацией. Ќасто€щие заметки приурочены к недавно прошедшему 80-летнему юбилею по€влени€ этой классической статьи »зинга.
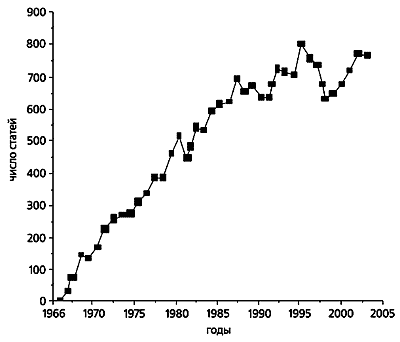
≈жегодное количество публикаций, посв€щенных модели »зинга после 1966 г.
(общее число публикаций за 1966-2003 гг. - около 20 тыс.).ћодель »зинга I
ѕрежде всего напомним суть модели. ак известно, магнетизм различных тел св€зан с магнитными свойствами атомов, составл€ющих данное тело. Ёти свойства, в свою очередь, обусловлены магнитными характеристиками электронов, вход€щих в состав атомов. “ак же как наиболее важным пунктом Уэлектрического паспортаФ электрона €вл€етс€ его электрический зар€д, Увизитной карточкойФ его магнитных качеств служит собственный магнитный момент (спин). ¬ отличие от зар€да, магнитный момент характеризуетс€ не только величиной, но и направлением (т.е. €вл€етс€ вектором). ќбычно магнитные моменты электронов направлены в разные стороны, так что их сумма (векторна€) практически равна нулю. ќднако в некоторых случа€х магнитные моменты значительной части электронов станов€тс€ параллельными друг другу. “огда и возникает сильный магнетизм, или, как его обычно называют, - ферромагнетизм (от лат. ferrum - железо).
ѕричина такого выстраивани€ магнитных моментов электронов - их взаимодействие друг с другом. “акое взаимодействие может быть пр€мым (без вс€ких УпосредниковФ) и косвенным (через УпосредниковФ, в качестве которых могут выступать другие электроны, свободные или вход€щие в состав атомов).
чему приводит пр€мое взаимодействие, можно пон€ть с помощью простых экспериментов с магнитными стрелками - чувствительными элементами прибора дл€ определени€ направлени€ магнитного пол€ «емли (компаса). ¬ отношении магнитных свойств такие стрелки очень похожи на электроны: они обладают собственным магнитным моментом (направленным вдоль оси стрелки от УюжногоФ полюса к УсеверномуФ), ориентаци€ в пространстве которого мен€етс€ при вращении стрелки вокруг иглы.
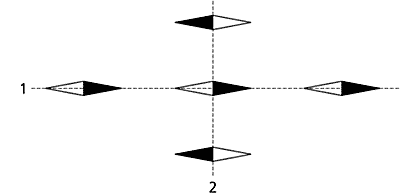
јнизотропное взаимодействие магнитных стрелок.
≈сли две стрелки поместить близко друг от друга, их взаимодействие становитс€ очень сильным и вли€нием магнитного пол€ «емли можно пренебречь. «акрепим одну из стрелок, например, сн€в ее с оси и приклеив к поверхности стола (фиксированную ориентацию этой стрелки будем далее называть выделенным направлением). Ќа этой поверхности нарисуем две пр€мые линии, проход€щие через центр закрепленной стрелки: одну - вдоль выделенного направлени€ (лини€ 1), а другую - перпендикул€рно ему (лини€ 2). Ѕудем теперь приближать к неподвижной стрелке другую магнитную стрелку, способную вращатьс€ вокруг иглы. ≈сли в процессе этого приближени€ центр второй стрелки все врем€ остаетс€ на линии 1, то (независимо от начальной ориентации) эта стрелка рано или поздно встанет так, что магнитные моменты обеих стрелок будут параллельными. ≈сли же в процессе приближени€ второй стрелки ее центр все врем€ остаетс€ на линии 2, то она в конце концов ориентируетс€ так, что магнитные моменты обеих стрелок станут антипараллельными. Ёти эксперименты показывают, что в отличие от электрического (кулоновского) взаимодействи€ между электрическими зар€дами, завис€щего только от знаков этих зар€дов и рассто€ни€ между ними, пр€мое взаимодействие магнитных моментов зависит еще и от угла, который соедин€юща€ их лини€ составл€ет с выделенным направлением.
освенное взаимодействие магнитных моментов промоделировать трудно. ћожно лишь предположить, что при наличии УпосредниковФ зависимость энергии взаимодействи€ от указанного выше угла пропадает и остаетс€ лишь зависимость от рассто€ни€ между магнитными моментами и от их знаков (т.е. направлений). “очный расчет подтверждает это предположение *. “аким образом, дл€ определенности можно, например, считать, что взаимодействие всегда (независимо от взаимного расположени€) благопри€тствует параллельной ориентации магнитных моментов.
* ¬ качестве аналогии рассмотрим теннис, в котором взаимодействие игроков осуществл€етс€ напр€мую - с помощью м€ча, который доставл€ет игроку, принимающему подачу, ту информацию, что была вложена в него подающим игроком. ј вот в футболе м€ч, посланный в поле вратарем одной из команд, попадает к вратарю другой команды, испытав предварительно взаимодействие с дес€тком полевых игроков и полностью потер€в ту информацию, что была вложена в него первым вратарем.ѕредставим теперь, что магнитные стрелки (которые, напомним, моделируют магнитные моменты электронов) расположены в узлах регул€рной решетки. ѕоскольку взаимодействие быстро спадает с увеличением рассто€ни€, можно ограничитьс€ взаимодействием только соседних магнитных моментов. —огласно прин€тому предположению, такое взаимодействие благопри€тствует выстраиванию соседних магнитных моментов вдоль некоторого выделенного направлени€ и тем самым понижает энергию системы, внос€ в нее отрицательный вклад ЦJ. Ќаоборот, антипараллельна€ ориентаци€ соседних моментов энергетически невыгодна и приводит к увеличению энергии на величину J. Ёто и есть модель »зинга, в которую, однако, необходимо внести еще один элемент - тепловые флуктуации.ќчевидно, что при сделанных предположени€х наименьшей энергии системы соответствует состо€ние, в котором все магнитные стрелки параллельны друг другу. ќднако представим теперь, что стол, на котором размещены все эти стрелки, беспор€дочно тр€сетс€ (например, во врем€ землетр€сени€). ясно, что если така€ тр€ска станет достаточно сильной, ориентационный пор€док среди магнитных моментов стрелок исчезнет. Ќасто€щие же магнитные моменты отдельных электронов настолько малы, что не нуждаютс€ в землетр€сении: дл€ них достаточно всегда существующей тепловой Утр€скиФ решетки. ≈сли энерги€ ~kT, получаема€ ими от решетки, сравнима с энергией взаимодействи€ J, то в равновесном состо€нии полной ориентации магнитных моментов не будет. Ѕолее того, не€сно, сохранитс€ ли хот€ бы преимущественна€ ориентаци€ этих моментов?
ƒл€ ответа на этот вопрос и была предложена модель, которую называют моделью »зинга. ¬ ней магнитные моменты-спины, располагающиес€ в узлах регул€рной решетки, могут быть ориентированы только вдоль (или против) некоторого выделенного направлени€. ”читываетс€ лишь взаимодействие соседних спинов, энерги€ которого принимает (в зависимости от их взаимной ориентации) значени€ ±J. Ёта модель принципиально важна в том отношении, что относитс€ к системе, в которой наблюдаютс€ кооперативные €влени€ и фазовые переходы, и допускает математическое рассмотрение.
Ёрнст »зинг (1900-1998)
¬первые количественный анализ подобной модели был проведен в 1924 г. Ёрнстом »зингом в его докторской диссертации [1]. ¬ 1925 г. полученные им результаты были опубликованы * [2]. ∆изнь »зинга захватила практически весь прошлый век и включила в себ€ многие драматические событи€ политики и науки. ќ том, насколько важной оказалась модель »зинга дл€ последующего развити€ физики, свидетельствует хот€ бы тот факт, что уже после 1966 г. по€вилось около 20 тыс. публикаций со ссылкой на оригинальную работу »зинга и более 300 тыс. публикаций, использующих или развивающих эту модель. ќднако несмотр€ на грандиозную попул€рность модели »зинга, мало кто знает о самом ее авторе, в долгой жизни которого переплелось много трагического и счастливого. ќписанна€ в насто€щих заметках биографи€ »зинга в значительной мере основана на материалах работ [3-6].
* ∆урнал, где опубликована эта работа (написанна€ на немецком €зыке), малодоступен. ¬ »нтернете имеетс€ английска€ верси€ статьи в переводе ƒжоанны »зинг (жены Ё.»зинга, экономиста по специальности) и “ома аммингса (Thomas F.Cummings, химика по специальности), содержаща€ р€д неточностейЁрнст »зинг родилс€ 10 ма€ 1900 г. в ельне (√ермани€) в семье лавочника √устава »зинга и его жены “еклы (урожденной Ћоэве). ƒвум€ годами позже семь€ переехала в Ѕохум (¬естфали€), где Ёрнст и провел свое детство. ¬есной 1907 г. он поступил в местную школу, а в 1918 г. окончил гимназию. Ўла война, и Ёрнста призвали на военную подготовку, но, к счастью, перва€ мирова€ война закончилась раньше, чем он мог быть отправлен на фронт. ¬есной 1919 г. »зинг начал изучать математику и физику в √еттингенском университете, затем продолжил свое образование в Ѕонне и, начина€ с 1922 г., - в √амбурге.
(http://www.fh-augsburg.de/~harsch/anglica/Chronology/20thC/Ising/ isi\_fm00.html).¬ 20-е годы прошлого века √амбург был одним из центров развити€ мировой физической науки. «десь занимались исследовани€ми многие выдающиес€ ученые. ¬о врем€ учебы в √амбурге »зинг познакомилс€ со своим ровесником ¬ольфгангом ѕаули (1900-1958), который только что начал работать в том же университете в должности ассистент-профессора теоретической физики. ¬ марте 1924 г. ѕаули опубликовал статью, где был сформулирован один из важнейших принципов современной теоретической физики (в 1945 г. он получил Ќобелевскую премию Уза открытие принципа запрета, который называют принципом ѕаулиФ).
¬ это же врем€ в √амбурге работал ќтто Ўтерн (1888-1969), который стал полным профессором √амбургского университета в 1923 г. и вместе с ¬альтером √ерлахом (1889-1979) проводил свои знаменитые эксперименты с атомными пучками в неоднородном магнитном поле. ¬ 1943 г. ќтто Ўтерн (эмигрировавший к тому времени в —Ўј) был удостоен Ќобелевской премии Уза вклад в развитие метода молекул€рных пучков и открытие и измерение магнитного момента протонаФ.
«ан€тьс€ теоретической физикой предложил »зингу заведующий кафедрой теоретической физики √амбургского университета профессор ¬ильгельм Ћенц (1888-1957), помощником которого (с 1922 г.) был ѕаули. ѕод руководством Ћенца »зинг в 1922 г. начал исследовать одну из моделей ферромагнетизма, котора€ и стала темой его диссертации [1]. «ащита состо€лась в июле 1924 г. на факультете математики и естественных наук √амбургского университета.
ѕосле получени€ докторской степени »зинг переехал в Ѕерлин и в 1925Ц1926 гг. служил в патентном бюро компании УAllgemeine ElektrizitдtsgesellschaftФ (AEG). Ќеудовлетворенный этой работой, он решил стать учителем. ¬ течение года »зинг работал в известной школе-интернате в —алеме, но дл€ продвижени€ на педагогическом поприще надо было получить специальное образование. ѕоэтому в 1928 г. он возвращаетс€ в Ѕерлинский университет дл€ изучени€ философии и педагогики и в 1930 г. сдает государственный экзамен школьному совету по высшему образованию. ¬ том же году »зинг женитс€ на ƒжоанне Ёмер, докторе экономики, которую он встретил в Ѕерлине. ћолода€ супружеска€ пара переезжает в —траусберг возле Ѕерлина, где Ёрнст получает должность помощника преподавател€ в высшей школе - должность дл€ лиц, сдавших соответствующий экзамен, но еще не имеющих необходимого опыта. ѕозже он перезжает в √россен-на-ќдере (ныне - город росно в ѕольше), чтобы заменить заболевшего коллегу.
¬ 1933 г. к власти приходит √итлер, и вскоре государственные служащие-евреи лишаютс€ работы. Ќе избежал этой участи и Ёрнст »зинг. ¬ течение года он оставалс€ безработным, не счита€ временной работы в ѕариже в школе дл€ детей эмигрантов. ¬ 1934 г. »зинг находит новую работу в еврейской школе-интернате в апуте вблизи ѕотсдама. Ёта школа была основана прогрессивным педагогом-теоретиком √ертрудой ‘айертаг (1890-1943?); ее им€ носит сейчас одна из улиц ѕотсдама); р€дом находилс€ летний дом јльберта Ёйнштейна. огда Ёйнштейн в 1932 г. уехал в —Ўј, школа арендовала этот дом дл€ дополнительных зан€тий. ѕозже »зинг с удовольствием рассказывал, как он купалс€ в ванне Ёйнштейна, поскольку в его доме ванны не было.
¬ последующие годы число учеников возрастало, так как еврейских детей изгон€ли из общественных школ. ¬ 1937 г. »зинг становитс€ одним из руководителей школы. 10 но€бр€ 1938 г. во врем€ У’рустальной ночиФ - погромной акции, направленной против немецких евреев, - жители деревни, спровоцированные нацистами, подвергли школу полному разграблению. ¬оспитанники школы вместе с ее директором ‘айертаг и преподавател€ми спр€тались в ближайшем лесу. ѕочти через 60 лет оставшиес€ в живых вернулись на это место и, вспомина€ о былых событи€х, назвали их Уизгнанием из ра€Ф.
ѕосле погрома »зинг возвращаетс€ в Ѕерлин. 15 но€бр€ он отправл€ет в школьную администрацию ѕотсдама письмо, в котором пишет: У— 11 но€бр€ еврейска€ школа-интернат в апуте закрыта. ¬озобновление зан€тий в обозримом будущем невозможно. Ѕоюсь, что все бумаги и документы утрачены. ћой нынешний адрес: Ѕерлин-¬ильмерсдорф, ѕаретцерштрассе, 10 IV. »зингФ. ќтвета он не получил.
„ерез три мес€ца, ранним утром 27 €нвар€ 1939 г., »зинг был вызван в гестапо. “ам он подвергс€ четырехчасовому допросу и был освобожден только после того, как обещал покинуть √ерманию. –ешив эмигрировать в —Ўј, »зинг с женой отправл€ютс€ в Ћюксембург. ќднако им пришлось задержатьс€ там, ввиду ограниченной квоты дл€ эмигрантов. ¬ день, когда »зингу исполнилось сорок лет, германска€ арми€ оккупировала Ћюксембург и американский консулат был закрыт. „тобы выжить, супруги »зинг вынуждены были нан€тьс€ в прислуги.
—екретное письмо јдольфа Ёйхмана (€нварь 1942 г.) провозгласило полную депортацию евреев, за исключением тех, кто имел супругов немецкого происхождени€. ¬ соответствиии с этим правилом »зинг мог бы остатьс€ с семьей. Ќо его и остальных еврейских мужей нееврейских жен не выпустили из Ћюксембурга и заставили работать на германскую армию. — ма€ 1943 г. вплоть до освобождени€ осенью 1944 г. они занимались демонтажем железнодорожных путей на линии ћажино в Ћоррейне.
„ерез два года после окончани€ второй мировой войны »зинг с семьей покинул ≈вропу на борту грузового судна и в апреле 1947 г. прибыл в Ќью-…орк. Ќа этом закончилась перва€ половина его жизни.
Ёрнст »зинг
(приблизительно 1925 г.).»зинг читает лекцию
в ”ниверситете Ѕрэдли
(начало 70-х годов).¬ течение года он работал преподавателем в государственном педагогическом колледже в ћиноте (—еверна€ ƒакота), а в 1948 г. получил должность профессора физики в университете Ѕрэдли в ѕеории (»ллинойс), где и преподавал вплоть до ухода на пенсию в 1976 г. √ражданство —Ўј и им€ Ёрнест он получил в 1953 г. «десь, в провинциальной ѕеории, прошла втора€, гораздо более счастлива€ половина жизни »зинга.
ѕосле ¬торой мировой войны ѕаули попросил своего коллегу ¬алентина “елегди навести справки о выживших физиках. »зинг был УобнаруженФ, и в феврале 1951 г. ѕаули написал ему: Уƒорогой м-р »зинг, спасибо за ваше письмо. я рад узнать, что ¬ы пережили гитлеровскую УжизньФ и нашли работуЕФ
”влечением »зинга в послевоенные годы стало преподавание. ≈го ученики помн€т проводимые им на лекци€х тщательные демонстрационные опыты и свойственный лектору тонкий юмор. ќн говорил, что урок нельз€ считать успешным, если в ходе его ученики хот€ бы один раз не рассме€лись. ќн любил из€щные искусства и поэзию и даже в преклонные годы мог цитировать √ете и других немецких классиков. Ёто, по-видимому, нашло отражение в еще одной (научно-попул€рной) публикации »зинга У√Єте как физикФ [7].
»зинг любил спорт, особенно туризм и плавание. ¬ 1980 г. (в 80-летнем возрасте!) он с женой участвовал в лед€ном шоу ƒороти ’эмилл, золотой медалистки ќлимпийских »гр. ќни вместе танцевали вальс. роме того, он был страстным фотографом. » до, и после выхода на пенсию он много путешествовал, побывал почти во всех американских штатах и посетил многие страны мира.
¬ течение долгих лет »зинг не принимал никакого участи€ в научной жизни и только в 1949 г. узнал о широкой известности своей статьи. ќн изумл€лс€ каждый раз, когда в публикаци€х упоминалась его им€, но будучи человеком скромным, всегда отмечал вклад своего руководител€. ¬ одном из писем он писал: Уя хочу обратить внимание, что эта модель должна на самом деле называтьс€ моделью Ћенца-»зинга. »де€ принадлежала моему наставнику доктору ¬ильгельму Ћенцу, который предложил мне исследовать ее математически в моей диссертацииЕФ.
Ёрнст »зинг умер 11 ма€ 1998 г. в своем доме в ѕеории на следующий день после своего 98-го дн€ рождени€.
ћодель »зинга II
онцепци€ микроскопической модели магнитной системы, состо€щей из элементарных магнитных моментов с двум€ возможными ориентаци€ми УвверхФ и УвнизФ, была предложена ¬ильгельмом Ћенцем. ќн впервые использовал эту модель дл€ объ€снени€ парамагнитных свойств твердых тел [8]. ¬ конце своей статьи он следующими словами сформулировал идею взаимодействи€: Уѕредположение о том, что потенциальна€ энерги€ взаимодействи€ атома (элементарного магнита) в ферромагнетике с его сосед€ми в положении У0Ф отличаетс€ от таковой в положении УpФ, приводит к выводу о естественной ориентации атомов и возникновению спонтанной намагниченностиЕ ћожно наде€тьс€, что таким образом удастс€ объ€снить свойства ферромагнетиковФ.

¬ильгельм Ћенц (1888-1957).
¬ своей диссертации [1] »зинг рассмотрел частный случай линейной цепочки магнитных моментов, св€занных взаимодействием с ближайшими сосед€ми. ќн показал, что спонтанную намагниченность нельз€ объ€снить в рамках такой одномерной модели. ¬ статье [2], написанной по материалам диссертации, он ошибочно обобщил полученный результат и на трехмерный случай.
»зинг знал о первой ссылке на его работу в статье √ейзенберга [9], в которой тот ввел квантовомеханическое обменное взаимодействие дл€ описани€ ферромагнетизма. √ейзенберг писал: Уƒругие сложности детально обсудил Ћенц, а »зингу удалось показать, что и предположение о наличии достаточно больших сил между любыми двум€ соседними атомами цепочки не объ€сн€ет по€влени€ ферромагнетизмаФ.
—тефен Ѕраш, автор опубликованного в 1967 г. обзора [10], посв€щенного модели »зинга, так комментирует этот пассаж √ейзенберга: У“аким образом, √ейзенберг использовал предполагаемую несосто€тельность модели Ћенца-»зинга дл€ объ€снени€ ферромагнетизма как оправдание дл€ разработки своей собственной теории, основанной на более сложном взаимодействии между спинами. Ёто привело к опрокидыванию естественного пор€дка развити€ теории ферромагнетизма: сначала рассматривалась более изощренна€ модель √ейзенберга и только затем теоретики все-таки вернулись к исследованию свойств более простой модели Ћенца-»зингаФ.
“ермин Умодель »зингаФ ввел, по-видимому, –удольф ѕайерлс в своей статье 1936 года [11], котора€ называлась Уќ модели ферромагнетизма »зингаФ. ќн рассмотрел границу, котора€ раздел€ет области со спинами УвверхФ и УвнизФ в двумерной квадратной решетке »зинга. ќценив верхний предел длины замкнутых границ, он показал, что при достаточно низких температурах лишь мала€ дол€ от общего числа спинов заключена внутри областей, ограниченных такими границами. —ледовательно, большинство спинов должно иметь противоположный знак, что означает спонтанную намагниченность системы.
Ќаиболее впечатл€ющий успех модели »зинга св€зан с иссследованием фазового перехода между ферромагнитным и парамагнитным состо€ни€ми. Ќасто€щий прорыв произошел, когда различные авторы обнаружили, что проблему можно сформулировать в матричном представлении, в котором свойства системы св€заны с так называемыми собственными значениеми некоторой матрицы [12, 13].
’ендрик рамерс и √регори ¬анье [12] нашли численное значение температуры TC, при которой в двумерной изинговской системе возникает отличный от нул€ суммарный магнитный момент (так называема€ температура юри): kTс = 2.27J, а точное и полное ее решение (дл€ пр€моугольной решетки) было получено в 1944 г. Ћарсом ќнзагером [14].
¬ насто€щее врем€ известны также точные решени€ двумерной проблемы »зинга дл€ треугольной и шестиугольной решеток и решетки Ѕете *, а также дл€ так называемой модели льда на квадратной решетке (она же - шестивершинна€ модель) и восьмивершинной модели [15].
* Ёта решетка строитс€ с помощью специальной процедуры и не €вл€етс€ решеткой в обычном смысле этого слова. ќна напоминает ветвистое дерево, в котором от каждой развилки отходит одинаковое количество ветвей. аждый узел в такой решетке св€зан с одинаковым числом соседей, но в ней нет замкнутых путей.¬ модели льда решетка состоит из атомов двух сортов (условно - УкислородФ и УводородФ), первые из которых занимают узлы квадратной решетки, а вторые расположены на св€з€х между ними. јтомы подчин€ютс€ Управилу льдаФ: из четырех водородных атомов, окружающих каждый кислородный атом, два (любые) расположены близко, а два других удалены вдоль линий соответствующих св€зей. У¬одородна€Ф св€зь между атомами кислорода осуществл€етс€ через атомы водорода. ¬ модели »зинга этим св€з€м соответствуют магнитные моменты, которые можно изображать стрелками, параллельными лини€м св€зи и направленными к тому концу св€зи, который зан€т атомом водорода. Уѕравило льдаФ сводитс€ к утверждению, что у каждого узла (где расположен атом кислорода) имеютс€ два момента, направленные к нему, и два момента, направленные от него. ¬сего имеетс€ шесть различных конфигураций стрелок, удовлетвор€ющих этому правилу (поэтому модель типа льда называют иногда шестивершинной моделью) с энерги€ми, которые, вообще говор€, могут быть все отличны друг от друга. ¬се шесть допустимых конфигураций стрелок-диполей у вершины представлены на рисунке.

–азличные комбинации ориентаций диполей в шестивершинной модели.
¬осьмивершинна€ модель - обобщение модели льда. ¬ ней к приведенным выше шести конфигураци€м стрелок вокруг узла добавл€ютс€ еще две, в которых все стрелки вход€т в узел или выход€т из него (очевидно, дл€ таких узлов правило льда не выполн€етс€).
„то касаетс€ трехмерной модели »зинга, то, несмотр€ на многочисленные попытки, найти ее точное решение до сих пор не удалось (согласно приближенным аналитическим и компьютерным расчетам, kTс ~ 4.5J). Ѕолее того, недавно по€вились строгие математические аргументы в пользу того, что точно решить эту проблему вообще невозможно [16]. јвтор этого утверждени€ —орин »стрейл (директор отдела информатики в Celera/Applied Biosystems, Rockville, MD) говорит: У онечно, это не так полезно, как найти чашу √раал€. ¬сем бы нам хотелось быть похожими на Ћарса ќнзагера. Ќо, по крайней мере, теперь никому не надо тратить врем€ на решение неразрешимой задачиФ.
ћодель »зинга III
¬се, о чем мы говорили до сих пор, относилось к регул€рным решеткам магнитных моментов-спинов. –еальные же системы, свойства которых могут быть описаны в рамках модели »зинга, редко бывают абсолютно регул€рными. —уществует много причин, нарушающих строгую периодичность таких систем. ќдна из них - случайное замещение магнитных моментов, составл€ющих решетку, магнитными моментами другой величины. Ёто приводит к тому, что энерги€ взаимодействи€ параллельных спинов, в отсутствие подобных УпримесейФ равна€ ЦJ, случайным образом (с веро€тностью, равной относительной концентрации примесей) может принимать другое значение: ЦJҐ. ясно, что если в обоих случа€х энергетически выгодным €вл€етс€ параллельна€ ориентаци€ спинов (т.е. J, JҐ > 0), то примеси лишь повли€ют на температуру юри, ниже которой система по-прежнему будет ферромагнитной.
—ложнее обстоит дело, когда взаимодействие с примес€ми имеет антиферромагнитный характер (т.е. JҐ < 0). ћожно ожидать, что ферромагнитное состо€ние в такой системе возможно лишь до тех пор, пока концентраци€ антиферромагнитных примесей не достигнет некоторой критической величины. » это действительно так, однако оказываетс€, что критическа€ концентраци€ определ€етс€ особым механизмом - перкол€цией, котора€ обеспечивает существование св€занной области ферромагнитных спинов. ѕеркол€ци€ в значительной мере ответственна и за свойства системы, в которой нет примесей, но часть св€зей случайным образом удалена. ‘ормально это соответствует случаю JҐ = 0.
¬ последнее врем€ интенсивно исследуютс€ изинговские системы, в которых, наоборот, случайным образом устанавливаютс€ дополнительные (по отношению к существующим в регул€рной решетке) св€зи. ѕричем длина таких дополнительных св€зей также случайна - они могут обеспечивать взаимодействие спинов в узлах, очень далеко отсто€щих друг от друга. “ака€ нерегул€рна€ система называетс€ сетью Утесного мираФ. Ёто название - вольный перевод английского словосочетани€ small world network, относ€щегос€ к сет€м с особыми свойствами. ќдно из них, известное как Управило шести рукопожатийФ [17], состоит в том, что любые два человека на «емле знакомы друг с другом через шесть УпосредниковФ. јнглийское изречение УIt is a small world!Ф, св€занное с удивительно высокой веро€тностью того, что два любых человека имеют общих знакомых, имеет русский эквивалент У ак тесен мир!Ф, который и служит основанием дл€ приведенного варианта перевода. ¬ УобычныхФ сет€х (регул€рных и разупор€доченных) узлы соединены только со своими близкими сосед€ми. ¬ отличие от них, в Утесном миреФ имеютс€ случайные св€зи и между далекими (в геометрическом смысле) узлами. »менно наличие таких дальних св€зей (шунтов, или закороток) и обусловливает особые свойства таких сетей.
«адача »зинга в сети Утесного мираФ возникает так же, как в обычной решетке, - в узлах сети размещаютс€ изинговские спины, которые взаимодействуют (энерги€ взаимодействи€ J) лишь со своими ближайшими сосед€ми, т.е. с теми, которые непосредственно св€заны с выбранным спином. ќднако здесь УближайшимиФ станов€тс€ и некоторые геометрически удаленные спины, что, естественно, способствует магнитному упор€дочению. ќсновна€ задача здесь - определить, как температура юри зависит от доли p дальних св€зей.
“очное решение такой задачи известно лишь дл€ одномерной цепочки спинов. ¬ остальных случа€х она рассматриваетс€ путем компьютерного моделировани€. “ем не менее качественно верные и достаточно точные в количественном отношении результаты можно получить, распростран€€ на сети Утесного мираФ аргументы, высказанные ѕайерлсом еще в 1936 г. [11]. ≈го соображени€ свод€тс€ к оценке энергетической выгодности (или невыгодности) разбиени€ системы изинговских спинов на области (домены), внутри которых все спины параллельны, но их направление мен€етс€ при переходе через границу домена.
ќсобенно проста така€ оценка дл€ одномерной системы, где вблизи доменной границы расположена всего одна пара спинов, чь€ антипараллельна€ ориентаци€ увеличивает энергию системы на 2J. азалось бы, это преп€тствует образованию такой границы, а значит, и нарушению ферромагнитного пор€дка в системе. ќднако при конечной температуре термодинамически равновесное состо€ние, как известно, - это не состо€ние с наименьшей (внутренней) энергией, а наиболее веро€тное состо€ние *. ¬еро€тность же состо€ни€ тем больше, чем боШльшим числом способов оно (это состо€ние) может быть реализовано. ¬ рассматриваемом случае одномерной цепочки ферромагнитное состо€ние, в котором все спины параллельны друг другу, реализуетс€ единственным способом. —осто€ние же с одной доменной границей может реализоватьс€ большим числом способов, поскольку така€ граница может располагатьс€ в любом узле цепочки. ѕоэтому веро€тность по€влени€ доменов велика. Ёто перевешивает энергетический проигрыш 2J и приводит к тому, что ферромагнитное состо€ние не €вл€етс€ термодинамически равновесным. ‘ормально данному случаю соответствует Tс = 0.
* “очнее - состо€ние (при посто€нных температуре и объеме), соответствующее минимуму так называемой свободной энергии, котора€ меньше внутренней энергии системы на величину, тем большую, чем выше веро€тность конфигурации, соответствующей тому или иному состо€нию системы.¬ сети Утесного мираФ возможности размещени€ доменной границы значительно сужаютс€. ƒействительно, чтобы энерги€ системы не увеличилась, така€ граница не должна разрывать дальние св€зи. ¬ результате число допустимых конфигураций с доменной границей падает, и термодинамически равновесное ферромагнитное состо€ние восстанавливаетс€ (т.е. Tс > 0). ќценки дают дл€ одномерной цепочки спинов такую зависимость температуры юри от доли p дальних св€зей: Tс ~2Jln|p| (результат справедлив, если pN >> 1, где N - число спинов в цепочке).¬ двумерной и трехмерной регул€рных системах без дальних св€зей упор€доченное магнитное состо€ние существует (т.е. Tс > 0). ¬ведение дальних св€зей приводит лишь к росту температуры юри на некоторую величину DTс, завис€щую от p. –аспростран€€ описанные соображени€ на эти случаи, можно показать, что DTс ~ p1/2 дл€ двумерной системы и DTс ~ p2/3 дл€ трехмерной системы [18, 19]. Ёти выводы подтверждаютс€ компьютерным моделированием.
—истема, которую называют сетью Утесного мираФ, - математическа€ абстракци€. ¬озникает вопрос, существуют ли реальные физические объекты, устроенные таким образом? ќтвет на него попыталась дать четверка студентов из американского ”ниверситета ћиссисипи [20]. ќни приобрели в ювелирной лавочке длинное ожерелье - нить, на которую было нанизано N = 150 бусинок, и использовали его как модель одномерной регул€рной цепочки. ¬се бусинки были пронумерованы, после чего нить была случайным образом см€та и превращена в комок, что, конечно, не нарушило ее одномерности. ќднако после этого соседними оказались некоторые бусинки, которые до того находились далеко друг от друга, что эквивалентно введению дополнительных дальнодействующих св€зей. «атем была составлена таблица (так называема€ лапласиан-матрица) размером N і N, элемент которой, сто€щий на пересечении i-го столбца с j-й строкой, был равен 1 или 0, в зависимости от того, соседствуют ли друг с другом i-€ и j-€ бусинки.

ћодель сети Утесного мираФ.
“очно такой же эксперимент был произведен c помощью компьютера, который по специальному веро€тностному алгоритму УсоздалФ виртуальную одномерную систему Утесного мираФ. ќказалось, что некотора€ важна€ характеристика лапласиан-матриц (а именно, распределение их собственных значений) одинакова дл€ реальной и виртуальной систем. “а же характеристика дл€ исходной (пр€молинейной) цепочки - совсем ина€.
Ётот эксперимент показал, что макроскопические системы сети Утесного мираФ вполне реальны. ћожно думать, что реальны и микроскопические системы, в которых роль бусинок исполн€ют атомы или молекулы. Ќе исключено, что они могут быть созданы из длинных (полимерных) молекул примерно по той же схеме, что описана выше.
¬веденна€ изначально дл€ понимани€ природы ферромагнетизма, модель »зинга оказалась в центре разнообразных физических теорий, относ€щихс€ к критическим €влени€м, жидкост€м и растворам, спиновым стеклам, клеточным мембранам, моделированию иммунной системы, различным общественным €влени€м и т.д. роме того, эта модель служит полигоном дл€ проверки методов численного моделировани€ различных физических €влений. * * *

«аметка в записной книжке »зинга со ссылкой на обзор G.F.Newell, E.W. Montroll
(Rev. Mod. Phys. 1953. V.25. є2. P.353-389)—ама€ больша€ загадка »зинга - почему столь успешное начало научной де€тельности не получило никакого продолжени€? ќдно из возможных объ€снений состоит в том, что своей работой »зинг, как ему казалось, УзакрылФ возможность описани€ ферромагнетизма в рамках рассмотренной им модели. Ќедаром √ейзенберг, ссыла€сь в 1928 г. на результат »зинга, подчеркнул именно этот негативный вывод. » все же робкое за€вление »зинга о том, что его работа УЕдолжна представл€ть интерес дл€ проблемы ферромагнетизмаЕФ, которое он сделал в заключительной фразе своей статьи, оказалось пророческим. сожалению, первое УположительноеФ упоминание модели, использованной »зингом, как возможной основы дл€ объ€снени€ ферромагнетизма по€вилось только в 1936 г. в упоминавшейс€ выше работе ѕайерлса. Ќо в это страшное дл€ √ермании врем€ »зинг был слишком зан€т сохранением еврейской школы в апуте, а позже - и самой своей жизни. ѕоэтому вс€ последующа€ истори€ модели »зинга прошла без участи€ самого »зинга.
–абота выполнена при поддержке –оссийского фонда фундаментальных исследований. ѕроект 06-02-16313.
Ћитература
1. Ising E. Beitrag zur Theorie des Ferro- und Paramagnetismus. Hamburg, 1924. ѕолный текст диссертации Ё.»зинга можно найти в »нтернете (http://www.fh-augsburg.de/~harsch/germanica/Chronologie/20Jh/Ising/isi\_fe00.html).
2. Ising E. // Zeitschrift f. Physik. 1925. Bd.31. S.253-258.
3. Fry L. The Isings and the 20th Century. Peoria, 1991. P.4.
4. Kobe S. // Physikalische Blatter. 1995. Bd.51. S.426.
5. Kobe S. // J. Stat. Phys. 1997. V.88. P.991-995.
6. Kobe S. // Braz. J. Phys. 2000. V.30. є4. P.649-654.
7. Ising E. // American J. Physics. 1950. V.18. P.235-236.
8. Lenz W. // Phys. Zeitschrift. 1920. Bd.21. S.613-615.
9. Heisenberg W. // Zeitschrift f. Physik. 1928. Bd.49. S.619-636.
10. Brush S.G. // Rev. Mod. Phys. 1967. V.39. P.883-893.
11. Peierls R. // Proc. Cambridge Phil. Soc. 1936. V.32. P.477-481.
12. Kramers H.A., Wannier G.H. // Phys. Rev. 1941. V.60. P.252-262.
13. Montroll E. // J. Chem. Phys. 1942. V.10. P.61-77.
14. Onsager L. // Phys. Rev. 1944. V.65. P.117-149.
15. Ѕэкстер –. “очно решаемые модели в статистической механике. ћ., 1985.
16. Istrail S. // Proceedings of the Thirty-Second Annual ACM Symposium on Theory of Computing. May 21-23. Portland, 2000. P.87-96.
17. Milgram S. // Psychol. Today. 1967. V.1. P.61-67.
18. Meilikhov E.Z., Farzetdinova R.M. // Phys. Rev. E. 2005. V.71. P.046111(1-8).
19. Meilikhov E.Z., Farzetdinova R.M. // e-Print arXiv:Cond-mat/0505502
20. e-Print arXiv:Cond-mat/0410589 v1/22 Oct 2004