є 3, 2007 г.
© ѕелиновский ≈.Ќ., —люн€ев ј.¬.
У‘рикиФ - морские волны-убийцы
≈.Ќ.ѕелиновский, ј.¬.—люн€ев
≈фим Ќаумович ѕелиновский, д. ф.-м.н., проф., гл. н. с. лаб. нелинейных геофизических процессов »ѕ‘ –јЌ,
проф. Ќижегородского государственного технического университета.јлексей ¬икторович —люн€ев, к.ф.-м.н., с.н.с. той же лаборатории.
явление, о котором пойдет речь, в англо€зычной литературе чаще всего обозначают термином freak waves *. ѕомимо него, существует множество других названий, отражающих изумление и страх: rogue waves, cape rollers, rabid-dog waves, abnormal waves, exceptional waves, giant waves, steep wave events. ¬ русском €зыке внезапно возникающие неожиданно высокие волны на морской поверхности называют аномально высокими, экстремальными, волнами-шатунами, либо просто убийцами. ≈ще совсем недавно их существование подвергалось сомнению, несмотр€ на значительное число свидетельств случайных очевидцев. ќднако с по€влением инструментальных измерений наличие проблемы стало бесспорным и породило огромное число исследований в последние 10-15 лет. ¬ –оссии над проблемой волн-убийц активно работает несколько групп, в том числе в »нституте прикладной физики –јЌ.
* Freak - необычный, причудливый; freak waves - волны блуждающие.¬олны: высокие и аномальные¬олна в океане может быть большой. ≈е высота может достигать полукилометра, как произошло в 1958 г. на јл€ске, когда мощный оползень в маленькой бухте произвел эффект падающего куска сахара в стакане. ¬озникша€ волна просто захлестнула противоположный берег, смыв с него лесной покров и выбросив на берег сто€вшие в бухте суда [1]. ѕон€тно, что схожую картину можно ожидать и от падени€ крупных астероидов, но подобные источники генерации волн €вл€ютс€ экстраординарными и крайне редкими. “акие волны относ€тс€ к разр€ду цунами; не нужно загл€дывать далеко в историю за примерами их разрушительного действи€: достаточно вспомнить индонезийское цунами 2004 года.
—уществует большое количество менее экзотических по происхождению волн на поверхности ћирового океана, обусловленных действием гравитации, силой ориолиса (следствие того, что точки разных широт на поверхности «емли имеют различные радиусы вращени€), эффектами захвата неровност€ми дна и др. ¬олны, которые мы обычно наблюдаем на море, - гравитационные волны, возникшие под действием ветра. Ќа больших дистанци€х или в штормовых област€х ветер создает наиболее интенсивные волны; потом они могут убегать из зоны генерации, несколько измен€€сь из-за различного закона ослаблени€ волн разной длины (такие волны называютс€ зыбью).
роме интенсивности (она характеризуетс€ высотой волны H - рассто€нием по вертикали от дна ложбины до пика гребн€), важна длина волны l. ќтношение этих двух величин дл€ индивидуальной волны задает ее крутизну k:
k = p (H/l) (1)
¬олна не может быть слишком крутой. ѕри достижении определенного порогового значени€ она начинает обрушиватьс€ подобно тому, как осыпаетс€ слишком крутой песчаный бархан. ƒлина волны св€зана с периодом T через дисперсионное соотношение, куда дл€ гравитационных свободных волн помимо величины ускорени€ свободного падени€ g входит зависимость от глубины мор€ D:
w = ÷kg th(kD), w = 2pT-1, k = 2pl-1. (2)
“ипична€ крутизна морских волн составл€ет 0.07-0.1. Ќетрудно видеть, что дл€ волн на глубокой воде (kD >> 1) с периодом 10-12 с это соответствует высоте 3.5-7 м. “акой период волн характерен дл€ хорошо развитого волнени€, волны с меньшим периодом оказываютс€ ниже по высоте. ќбрушивающимис€ в приведенном примере станов€тс€ 20-30-метровые волны; обрушение ограничивает их возможные высоты и приводит к перераспределению энергии между волнами разных масштабов. –еально зарегистрированные волны в штормовых районах действительно достигают высоты
30 м. Ёти волны ростом с дес€тиэтажный дом, несомненно, очень опасны. ќднако дл€ адекватной оценки опасности €влени€ необходимо знать еще одну величину - его веро€тность, т.е. как часто можно ожидать столь губительную волну. Ќапример, по существующим представлени€м, в Ѕаренцевом море возможны волны высотой 24 м, а в —еверном море - 30 м лишь один раз в 100 лет.
ќтвет на вопрос о частоте повтор€емости экстремальных волн призваны давать статистические теории. ќни описывают не индивидуальные волны, а их ансамбли и способны прогнозировать веро€тность по€влени€ волн с заданными характеристиками, если известны некоторые усредненные параметры волнени€. Ќаиболее существенную роль в этом смысле играет значительна€ * высота волн Hs. ¬ рамках классической статистической модели веро€тность высот волн задаетс€ распределением –эле€
P(H) ~ exp(-2 H2/Hs2). (3)
‘ормула (3), основанна€ на центральной предельной теореме, провер€лась на большом статистическом материале и во многих случа€х дает очень хорошее описание. ¬идно, что веро€тность по€влени€ высоких волн экспоненциально спадает, т.е. они должны быть очень редкими. ƒействительно, число измеренных волн с большим превышением средней высоты H/Hs мало, что ведет к недостаточной степени верификации формулы (3) (а значит, и достоверности) в области экспоненциальных УхвостовФ.
* «начительна€ высота волн - средн€€ высота трети наиболее высоких волн в записи.ћорские описани€ богаты упоминани€ми о волнах-убийцах (Утри сестрыФ, Удев€тый валФ, Устена водыФ, Удыра в мореФ), которые традиционно относились скорее к фольклору, нежели к реальному положению вещей. ѕон€тно, что волны высотой с современный дом должны были приводить в ужас мореплавателей в прошлом. Ќесмотр€ на стремительный рост размеров и мощности кораблей и морских сооружений, ветровые волны продолжают быть разрушительными, привод€ к серьезным повреждени€м судов, гибели людей, а иногда и кораблей целиком. “ак, за период 1969-1994 гг. 22 супертанкера были потер€ны или существенно повреждены в “ихом и јтлантическом океанах; при этом погибло 525 человек, см. схему на рис.1 [2]. ак минимум 12 схожих случаев известны дл€ »ндийского океана около побережь€ ёжной јфрики [3]. √еографически места аварий судов коррелируют с основными судоходными пут€ми в океане; обработка немецким аэрокосмическим центром наблюдений морской поверхности с ≈вропейского космического спутника показывает, что наиболее интенсивные волны гул€ют на больших акватори€х (где разгон волн, а значит и способность ветра передавать энергию волнам, велики).

–ис. 1. —татистика встреч супертанкеров с волнами-убийцами за 1968-1994 гг. [2].
јргументированно говорить о высоких волнах стало возможным, когда с помощью буев или стационарных высотомеров начали вести записи последовательных измерений смещени€ поверхности воды. Ќаиболее интересны случаи внезапного возникновени€ высоких волн, значительно превосход€щих окружающие. ѕример такой записи дан на рис.2; она сделана у побережь€ √еленджика в „ерном море и демонстрирует максимально известное нам усиление волны по отношению к среднему уровню [4]: A = H/Hs ~ 3,9.

–ис. 2. ¬ременнA€ запись аномально высокой волны в „ерном море, полученна€ 22 но€бр€ 2001 г. [4].
≈сли в формулу (3) подставить H = 3Hs, получим, что така€ волна (дл€ характерного периода ветровых волн 10 с) может наблюдатьс€ один раз в 20 лет. “ем не менее, за уже упом€нутое трехнедельное наблюдение морской поверхности из космоса наблюдалось усиление A = 2.9; за 793 ч наблюдений волн в —еверном море зарегистрировано A = 3.19 [5]. —толь неожиданно часта€ регистраци€ экстремальных волн привела к серьезному пересмотру классической статистической модели в области высоких волн (например, по данным [5], волна с параметром A = 3.19 оказалась в 300 раз более веро€тной, чем ожидалось).
¬олна, представленна€ на рис.2, не просто больша€, а именно внезапно больша€. ќна разительно выдел€етс€ из предшествующих и следующих за ней волн по высоте и форме, хот€ ее длительность остаетс€ типичной дл€ записи. Ётот факт умножает ее губительность. ѕриведем в качестве примера описание встречи с волной-убийцей российского танкера-рефрижератора У“аганрогский заливФ из книги [3].
Е27 апрел€ 1984 г. танкер следовал из »ндийского океана в юго-восточную јтлантику. ƒул 6-балльный северо-северо-восточный ветер. ¬ 05 ч ветер изменилс€ на юго-западный, стал постепенно усиливатьс€ и к 11 ч достиг силы 8 баллов. —разу после 12 ч было замечено ослабление ветра; в 12 ч 30 мин, согласно измерени€м, его скорость составила 15 м/c. “акой же силы ветер оставалс€ и в последующие три часа. ¬олнение мор€ после 12 ч тоже несколько уменьшилось и не превышало 6 баллов. ’од судна был сбавлен до самого малого, оно слушалось рул€ и хорошо УотыгрывалосьФ на волне. Ѕак и палуба водой не заливались. Ќеожиданно в 13 ч 01 мин носова€ часть судна несколько опустилась, и вдруг у самого форштевн€ под углом 10-15∞ к курсу судна был замечен гребень одиночной волны, котора€ возвышалась на 4-5 м над баком (фальшборт бака отсто€л от уровн€ воды на 11 м). √ребень мгновенно обрушилс€ на бак и накрыл работающих там матросов (один из них погиб). ћатросы рассказывали, что судно как бы плавно пошло вниз, скольз€ по волне, и УзарылосьФ в вертикальный срез ее фронтальной части. Ќикто удара не ощутил, волна плавно перекатилась через бак судна, накрыв его слоем воды толщиной более 2 м. Ќи вправо, ни влево продолжени€ волны не было.“аким образом, волна по€вилась внезапно, была неожиданно высокой и крутой. Ёти свойства формируют среди высоких волн особый класс - необычных, аномальных волн, волн-убийц. ѕоскольку многие их параметры остаютс€ неизвестными, само определение оказываетс€ довольно расплывчатым. „аще всего пользуютс€ амплитудным критерием выделени€ аномально высоких волн: A > 2. (4)≈му удовлетвор€ют несколько сотен известных инструментальных регистраций аномальных волн на морской поверхности. ¬опрос о форме волны также важен (волны разной формы могут оказывать различное по силе воздействие на корабли и морские сооружени€), но более сложен. ‘орма волны зависит от действующих физических механизмов, а при моделировании - от точности модели. ¬ дополнение к (4) предлагались более строгие критерии отбора аномальных волн, суживающие это пон€тие, но мы будем использовать только условие (4). Ќедавн€€ фотографи€ волны у побережь€ амчатки (рис.3) демонстрирует, насколько неординарной может быть волна-убийца. ѕо свидетельству фотографа, он наблюдал несколько подобных одиночных волн, которые по€вл€лись на времена пор€дка дес€тка секунд и пробегали около 50 м. ¬ случае с У“аганрогским заливомФ (а также в некоторых других сходных описани€х) отмечалс€ очень крутой передний склон волны с глубокой впадиной; така€ асимметри€ определ€ла особую опасность волны. Ќаоборот, дл€ волны на рис.3 заметной впадины у фронта не было. ¬ажно, что во многих описани€х волны-убийцы возникают на фоне почти спокойного мор€.

–ис. 3. ‘отографи€ волны, сделанна€ у мыса ќльга (юг роноцкого п-ова, амчатка) ¬.—околовским в июне 2006 г.
онечна€ цель исследований волн-убийц - определение их параметров и разработка методов прогноза. ƒл€ этого необходимо изучать их статистику в различных акватори€х ћирового океана в зависимости от многочисленных географических факторов (батиметрии морского дна, очертаний береговой линии, течений, циклонов, ураганов). ¬ажное место здесь принадлежит физике формировани€ волн-убийц. ѕон€в механизмы их зарождени€, ученые смогли бы районировать ћировой океан по степени риска, а также определить услови€, предшествующие по€влению волн-убийц.
ћеханизмы-претенденты и модели
ѕризнание проблемы аномально высоких волн вызвало всплеск интереса к высоким морским волнам вообще. ≈сли не использовать многие традиционные упрощени€, волны на морской поверхности оказываютс€ достаточно сложной системой: это трехмерный объект, включающий границу двух сред с потоками (ветром и течени€ми) и определенной долей перемешивани€. ¬олны, согласно (2), обладают дисперсией групповой скорости cgr(k) = dw/dk и нелинейны; наконец, водна€ толща неоднородна по многим параметрам и содержит движени€ разных масштабов. ¬ слишком огрубленных модел€х (а без упрощени€ невозможно понимание физики сложного процесса) могут тер€тьс€ эффекты, обусловливающие €вление волн-убийц. ѕоэтому главна€ теоретическа€ задача - пон€ть физические механизмы, способные приводить к существенному усилению волн в локальной области, и сформулировать соответствующие модели, описывающие процесс.
Ќаиболее просты и интуитивно пон€тны линейные модели, которые дл€ объ€снени€ аномально высоких волн были предложены первыми. ¬олны на воде несут в себе энергию - тем бOльшую, чем выше волны. ѕотому естественно ожидать, что процессы различного рода фокусировки волновой энергии могут порождать очень высокие волны. —концентрировать энергию различных волн в одной области можно, например, если сгон€ть их под разными углами (пространственна€, или геометрическа€ фокусировка - как оптических лучей). ≈ще один вариант - собрать волны вместе из-за разницы в скорости распространени€ индивидуальных волн (благодар€ уже упоминавшейс€ дисперсии групповой скорости - дисперсионна€ фокусировка). ƒл€ этого волны должны быть неоднородными: таковы различные системы волн (например, генерируемые в данной области ветровые волны плюс зыбь, приход€ща€ из другой области генерации) или неоднородные сонаправленные волны. ¬ариации в волновых параметрах могут вызыватьс€ переменными услови€ми распространени€ (батиметрией, течени€ми, прохождением сильных атмосферных фронтов).

–ис. 4. √руппова€ скорость волн, определенна€ по записи на рис.2.
Ќа рис. 4 приведен пример определени€ текущей групповой скорости в 20-минутной выборке поверхностных волн (она высчитывалась через дисперсионное соотношение (2) по найденному локальному периоду волн). ¬идно, как резко ее величина измен€етс€ внутри записи. “ака€ неоднородность приводит к посто€нному схождению-расхождению волн и в принципе способна обеспечивать их сильный рост. Ќа рис.5 показан результат лабораторного моделировани€ фокусировки волн в результате действи€ дисперсии [6]. —оздаваемый волнопродуктором цуг волн соответствует случаю, когда длинные (более быстрые) волны расположены позади коротких, а закон модул€ции частоты волн подобран таким образом, чтобы их схождение было максимальным (в теории - в одной точке и в один момент времени). ¬идно формирование фактически одиночной волны в момент максимального сжати€, котора€ затем обрушаетс€ из-за слишком большой крутизны. ƒисперсионна€ фокусировка - классический эффект линейной физики, хорошо известный в оптике. Ёффективность сжати€ частотно-модулированных пакетов поверхностных волн доказана в многочисленных лабораторных экспериментах, этот механизм часто используют в лотке дл€ получени€ интенсивных волн. ƒл€ создани€ частотной модул€ции в цуге реальных морских волн требуютс€ переменные вынуждающие силы или услови€ распространени€: например, сильное течение, переменна€ глубина, неоднородный ветер.

–ис. 5. ћоделирование сжати€ волнового пакета в результате дисперсии в лабораторном бассейне [6].¬ли€ние переменной батиметрии на распространение поверхностных волн превосходно демонстрирует фотографи€ на рис.6. —корость волн зависит от глубины (см. (2)), поэтому волны с более глубоких областей догон€ют волны на мелководье, и волновой фронт выт€гиваетс€ вдоль береговой линии. ѕо той же причине образуютс€ области схождени€ волн за обтекаемыми островами, что также хорошо заметно на рис.6. »скривление волнового фронта приводит к геометрической фокусировке волновой энергии; этот процесс может дополн€тьс€ дисперсионной фокусировкой либо действовать независимо. ѕроцесс дисперсионного сжати€ с геометрической подфокусировкой может проходить еще резче, чем в одномерном случае, что пон€тно на качественном уровне.

–ис. 6. »скривление волновых фронтов как следствие вли€ни€ переменной глубины и обтекани€ преп€тствий.
¬олны малой амплитуды слабо взаимодействуют, остава€сь почти линейными. ѕоэтому быстрый процесс роста волн оказываетс€ слабо чувствительным к УзашумлениюФ модулированного цуга другими волнами (рис.7 показывает фокусировку волн в присутствии сильной случайной компоненты дл€ случа€ двух координат x и y), и проста€ линейна€ модель зачастую удовлетворительно описывает эту динамику.
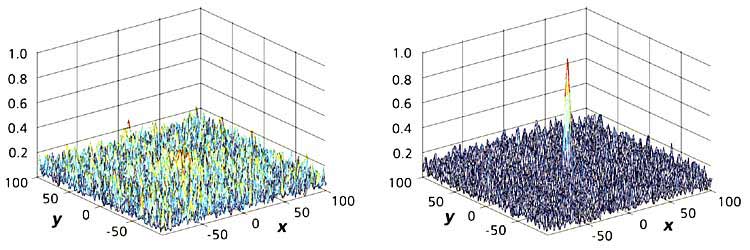
–ис. 7. „исленное моделирование дисперсионно-геометрического сжати€ в присутствии случайных волн:
начальное условие со Ђспр€таннойї частотной модул€цией (слева).
¬идна группировка у центра интенсивных (Ђкрасныхї) волн, но их амплитуда еще невелика.
ћомент образовани€ большой волны (справа) [8].¬заимодействие с сильными неоднородными течени€ми приводит к искажению траекторий волн и блокировке последних. ¬ простейшей модели поведение волн описываетс€ с помощью модифицированного дисперсионного соотношени€ (2) с учетом переменного течени€ и закона энергетического баланса - уравнени€ волнового действи€. «адачу можно нагл€дно интерпретировать на манер представлени€ потенциальной €мы (которое часто используетс€ в механике дл€ иллюстрации посто€нства суммы потенциальной и кинетической энергии и соответствующей динамики): запишем групповую скорость в приближении глубокой воды
cgr = dw/dk = 1/2 ÷g/k + U. (5)
Ќеоднородное течение U(x) здесь играет роль потенциальной €мы, вернее - наклонного барьера. ¬ полномерном случае U(x, y) - это Употенциальный оврагФ, в котором распростран€ютс€ волны. ќни не могут его покинуть, если склоны (перепад скорости течени€) слишком высоки, и распростран€ютс€ в среднем вдоль течени€ (€вление захвата волн), а также могут обращатьс€ всп€ть (блокировка волн течением). ѕри этом происходит перераспределение волновой энергии, по€вление областей ее концентрации (каустик); лучевые линии в поле течени€ ведут себ€, как показано на рис.8.

–ис. 8. ѕоведение лучевых линий волн на встречном течении, построенное дл€ района мыса »гольного [3].
«начительное усиление волны на встречном течении заметно в усть€х рек, когда морска€ волна заходит вверх по течению реки. —уществование областей схождени€ волн в результате действи€ течений, вли€ни€ переменной глубины, блокировки волн течени€ми повышает веро€тность по€влени€ высоких волн в этих точках, хот€ сами области фокусировки волновой энергии (каустики) могут случайно возникать и исчезать. ќписанный выше случай из книги [3] относитс€ к юго-восточному побережью јфрики, где вдоль материкового склона проходит сильное неоднородное течение мыса »гольного (јгуль€сово течение). –асчет лучевой картины дл€ описанных условий [3] показал наличие каустических точек с концентрацией волновой энергии (рис.8). —огласно наблюдени€м, волны-убийцы на течении мыса »гольного часто по€вл€ютс€ через несколько часов после того, как усиливающийс€ ветер измен€ет свое направление с северо-восточного на юго-восточное. ѕоскольку за формирование волн, систем разнонаправленных волн, модулированных волн ответственны атмосферные факторы, погодные закономерности напр€мую св€заны с созданием условий, благопри€тных дл€ по€влени€ волн-убийц, и должны изучатьс€.
Ёффекты нелинейности
ѕока речь шла о физических эффектах, которые описываютс€ линейными модел€ми. ¬ действительности морским волнам свойственна нелинейна€ динамика, €рким примером которой служит их обрушение. „тобы пон€ть происхождение эффектов нелинейности, достаточно осознать, что бегуща€ волна сама измен€ет услови€ распространени€, и чем она интенсивнее, тем значительнее это вли€ние. —тепень нелинейности однородных (монохроматических) волн определ€етс€ крутизной k. Ќелинейность в первую очередь модифицирует все фокусирующие механизмы [7, 8], поскольку скорость распространени€ волн становитс€ функцией их амплитуды, а также способствует эффективному взаимодействию отдельных волн. ¬озникают принципиально новые - нелинейные - механизмы генерации очень высоких волн.
ѕоверхностные волны подвержены многим нелинейным неустойчивост€м, когда малые возмущени€ могут стремительно нарастать. Ёто означает передачу энергии однородной системы волн волнам других масштабов и ведет к пространственному перераспределению волновой энергии и по€влению областей ее концентрации. Ќаиболее известна€ неустойчивость - эффект самомодул€ции волн на глубокой воде: однородные волны разбиваютс€ на долгоживущие св€занные группы. ’орошо известно €вление биени€ волн - сильна€ неоднородность пол€, состо€щего из суперпозиции волн двух близких частот. ¬ результате нелинейной неустойчивости энерги€ монохроматических волн передаетс€ двум другим системам волн - чуть большей и чуть меньшей частоты - и концентрируетс€ в област€х нелинейного фокуса. Ёффект управл€етс€ двум€ параметрами: крутизной и числом индивидуальных волн в группе, иначе амплитудой волн и длиной возмущени€ (которое всегда присутствует в реальности). Ќеустойчивыми станов€тс€ только достаточно длинные возмущени€; ими могут оказатьс€ волновые компоненты разных масштабов, и тогда волновое поле имеет очень сложный, в реальной задаче - хаотический характер.
ƒаже в случае однонаправленных волн развитие самофокусирующейс€ неустойчивости может перераспредел€ть энергию в поперечном направлении и формировать сильно локализованные трехмерные волновые группы и уединенные волны. Ёто св€зано со сложной диаграммой направлений и длин неустойчивых возмущений, котора€ также зависит от глубины места. ќписание одномерного процесса самомодул€ции (когда все волновые гребни выт€нуты в линию) в рамках простых теоретических моделей ограничивает усиление волн величиной A = 3; полнонелинейное численное моделирование говорит о несколько большем возможном усилении. ¬ полномерном случае это усиление может быть значительно боШльшим. Ќапример, на рис.9 волны в результате довольно сложного процесса развити€ модул€ционной неустойчивости вырастают более чем в семь раз [8] - таков результат численного моделировани€ нелинейного уравнени€ Ўредингера [9] дл€ случа€ двух поверхностных координат. ƒанное уравнение описывает модул€ции огибающей слабонелинейных волн (именно огибающа€ построена на рис.9). ѕомимо самомодул€ции монохроматических волн с плоским волновым фронтом теоретически изучаютс€ неустойчивости других, более сложных волновых систем. ѕроблема волн-убийц простимулировала исследовани€ неустойчивостей поверхностных волн; в частности, в работе [10] говоритс€ о значительно большем стабилизирующем вли€нии на процессы нелинейной самомодул€ции слабой диссипации волн, которой очень часто пренебрегают в теоретических и численных расчетах.

–ис. 9. –езультат развити€ модул€ционной неустойчивости. ѕоказана огибающа€ пол€.
Ќачальное условие - слабо возмущенный цуг волн единичной амплитуды [8].ћы проанализировали имеющиес€ записи аномально высоких волн в поисках св€занных нелинейных волновых групп - солитонов огибающей, использу€ подход на основе теории задачи рассе€ни€. ƒл€ всех 11 обработанных записей оказалось, что аномальна€ волна возникла на такой нелинейной группе, что свидетельствует о важной роли самомодул€ционных эффектов [11].
ѕроцессы генерации высоких волн с участием нелинейных неустойчивостей могут быть очень чувствительными к возмущени€м, а значит, трудно воспроизводимыми в лабораторном эксперименте и практически непредсказуемыми в реальном океане. Ќапример, волна-монстр с рис.9 не образуетс€ уже при слабом изменении начальных условий этого численного эксперимента. ѕотому здесь важно понимать потенциальные возможности усилени€ волн и определ€ть веро€тность таких процессов. ƒл€ первого необходимо развивать и изучать динамику волн в рамках наиболее реалистичных уравнений, а дл€ второго - анализировать статистику нелинейных волн.
ѕоследнее врем€ стало особенно плодотворным дл€ подобных исследований, так как посто€нное наращивание вычислительных мощностей современных компьютеров сопровождалось разработкой новых быстрых алгоритмов решени€ или исходных уравнений гидродинамики [12], или упрощенных, но очень аккуратных уравнений. ¬ результате численное моделирование не только оказываетс€ удобнее лабораторного эксперимента дл€ решени€ модельных задач, но и обретает способность давать результаты дл€ построени€ статистики. »спользование численного моделировани€ снимает проблему статистической однородности: реализации аномально высоких волн должны соответствовать одинаковым услови€м, что на практике не выполн€етс€ дл€ столь малого числа имеющихс€ измерений волн-убийц. —ейчас это направление интенсивно развиваетс€; моделирование вы€вило вли€ние нелинейности случайного волнового пол€ на функции распределени€. ¬ частности, функци€ распределени€ смещени€ поверхности становитс€ асимметричной (положительный третий момент), так что число больших гребней превышает число больших У€мФ, возникает зависимость четвертого момента (эксцесса, вли€ющего на долю высоких волн) от степени нелинейности ([13] и ссылки в статье). ¬еро€тностные свойства интенсивных волн можно также рассчитывать в рамках статистического подхода [14] или оценивать по запис€м волн и тем самым находить области ћирового океана, где аномально высокие волны наиболее веро€тны.
ѕо мере уменьшени€ глубины области неустойчивых возмущений сужаютс€ и физически отсутствуют в мелководном пределе (kD << 1 в (2)). ќднако и в этом случае волны не перестают быть нелинейными (и даже наоборот, сила нелинейных эффектов по отношению к дисперсионным возрастает). јномальные волны были зарегистрированы и на умеренных глубинах, и в услови€х мелководь€. «десь предложены сценарии возникновени€ аномальных волн в результате динамики нелинейных уединенных волн (солитонов), которые выгл€д€т как долгоживущие гребни волн, а также их взаимодействи€ с потоками.
ѕонимание механизмов образовани€ аномально высоких волн и моделирование их динамики отвечают на вопросы, где и когда ожидать такую волну, как она выгл€дит и эволюционирует. ћы численно промоделировали динамику аномальных волн на основе инструментальных регистраций. ’от€ запись волн в одной точке не описывает их развити€ (не определ€етс€, например, врем€ жизни волны-убийцы), приближенные эволюционные модели позвол€ют восполнить этот пробел: пересчитать запись в соседние пространственные точки так, словно по ходу волн были расположены другие самописцы. ѕо нашим расчетам, времена жизни измеренных волн-убийц оказались от нескольких секунд до полутора минут. “акое динамическое моделирование наиболее информативно, но требует много данных, причем с высокой точностью, а его результаты дл€ больших времен (или дистанций) могут сильно искажатьс€ из-за неустойчивостей. ѕоэтому в прогностических модел€х должны, очевидно, использоватьс€ кинетические модели, описывающие эволюцию спектра волн, динамическое же описание следует примен€ть дл€ получени€ параметров аномальных волн, важных дл€ разработки норм строительства безопасных кораблей и морских сооружений.
Ѕлизкие родственники
явление аномально высоких волн можно понимать шире; к нему можно отнести неожиданные заплески прибрежной зоны, которые не удаетс€ объ€снить выходом волн цунами либо приходом штормовых волн. “акие процессы известны, и в насто€щее врем€ их св€зывают, в частности, с динамикой краевых волн, распростран€ющихс€ вдоль берега [15]. «анимательна€ фотографи€ подобного эпизода приведена на рис.10. ћы начали собирать описани€ аномальных волн; этот материал может служить лучшему пониманию и классификации природного €влени€, однако, к сожалению, не всегда по-насто€щему достоверен.

–ис. 10. —лучай внезапного кратковременного затоплени€ берега на пл€же ћаракас (“ринидад и “обаго) в окт€бре 2005 г.
ѕредложенные дл€ объ€снени€ аномально высоких волн механизмы мы, конечно, изложили бегло и неполно; подробнее см. в монографии [16]. Ќесмотр€ на значительное число претендентов на роль родителей волн-убийц, они пока довольно оторваны от реальных наблюдений. ѕо всей видимости, в океане работают различные механизмы образовани€ Ђфриковї, но какие из них оказываютс€ наиболее распространенными, а какие практически не реализуемы - сегодн€ доподлинно неизвестно. “ем самым картина волны-убийцы остаетс€ незаконченной. ќбнаруженные сценарии генерации Ђпример€ютс€ї и на другие типы волн: внутренние волны, существующие в стратифицированном океане, захваченные топографией краевые волны, глобальные волны –оссби; возможны приложени€ этих теорий в физике плазмы, включа€ астрофизическую плазму, в оптике. Ќедавние случаи неожиданных столкновений высоких волн с крупными лайнерами и нефт€ными платформами привлекли к проблеме дополнительное внимание. сожалению, публикации в широкой прессе нар€ду со свежей информацией содержат много неточностей, а то и просто неверных данных. Ќо проблема продолжает свое развитие и стимулирует исследовани€ в смежных област€х.
–абота выполн€лась при поддержке –оссийского фонда фундаментальных исследований (проект 05-05-64265), »Ќ“ј— (грант 06-1000013-9236), ‘онда содействи€ отечественной науке и ведущей научной школы академика ¬.».“аланова.Ћитература 1. ѕелиновский ≈.Ќ. Ќелинейна€ динамика волн цунами. √орький, 1982.
2. Lawton G. // New Scientist. 2001. V.170. є2297. P.28-32.
3. Ћавренов ».¬. ћатематическое моделирование ветровых волн в пространственно-неоднородном океане. —ѕб., 1998.
4. ƒивинский Ѕ.¬., Ћевин Ѕ.¬., Ћопатухин Ћ.». и др. // ƒјЌ. 2004. “.395. є5. —.690-695.
5. Stansell P. // Applied Ocean Research. 2004. V.26. P.35-48.
6. Clauss G. // Appl. Ocean Research. 2002. V.24. P.147-161.
7. Pelinovsky E., Talipova T., Kharif C. // Physica D. 2000. V.147. є1-2. P.83-94.
8. Slunyaev A., Kharif C., Pelinovsky E., Talipova T. // Physica D. 2002. V.173. є1-2. P.77-96.
9. ќстровский Ћ.ј., ѕотапов ј.». ¬ведение в теорию модулированных волн. ћ., 2003.
10. Segur H., Henderson D., Carter J. et al. // J. Fluid Mech. 2005. V.539. P.229-271.
11. Slunyaev A., Pelinovsky E., Guedes Soares C. // Applied Ocean Research. 2005. V.27. P.12-22.
12. Dyachenko A.I., Zakharov V.E. // ѕисьма в ∆Ё“‘. 2005. “.81. є6. —.318-322.
13. Pelinovsky E., Sergeeva (Kokorina) A. // European J. of Mechanics B / Fluids. 2006. V.25. є4. P.425-434.
14. Janssen P.A.E.M. // J. Phys. Oceanogr. 2003. V.33. P.863-884.
15. Kurkin A., Pelinovsky E. // European J. of Mechanics B / Fluids. 2002. V.21. є5. P.561-577.
16. уркин ј.ј., ѕелиновский ≈.Ќ. ¬олны-убийцы: факты, теори€ и моделирование. Ќижний Ќовгород, 2004.