Январь
2002
|
|
90-летие
журнала
Январь 2002 |
© В.Г.СурдинГРАВИТАЦИЯ И ЗВЕЗДЫ
В.Г.Сурдин
Владимир Георгиевич Сурдин, кандидат физико-математических наук,
старший научный сотрудник Государственного астрономического института им.П.К.Штернберга.Главный персонаж Вселенной
Практически все, что мы видим в космосе, - это звезды, более или менее похожие на Солнце. Разумеется, существует вещество и вне звезд: планеты, их спутники, кометы и астероиды, межзвездные газ и пыль. Но все это - незначительный “довесок” к гигантским звездам, объединенным в агрегаты различного масштаба: от двойных систем до галактик и их скоплений. Правда, в последние годы появляется все больше аргументов, что во Вселенной присутствует небарионное вещество, состоящее не из протонов и нейтронов, а из частиц неясной пока природы; его взаимодействие с обычным веществом происходит только через силу гравитации [1]. Но даже если это необычное вещество действительно существует, обнаружить его удастся, лишь изучая поведение взаимодействующего с ним нормального вещества, т.е. звезд - главного наблюдаемого персонажа природы.
Вселенная не всегда состояла из звезд: более 10 млрд лет назад, когда от начала ее расширения прошло не более 300 тыс. лет, наш мир был заполнен очень горячим однородным веществом и излучением, причем по плотности энергии излучение превосходило вещество. Когда возраст Вселенной превысил 300 тыс. лет и наполняющая ее материя остыла примерно до 4000 К, плотность энергии излучения стала ниже, чем вещества, и с тех пор это различие только усугублялось. Но еще многие сотни миллионов лет после того, как вещество стало основным компонентом Вселенной, оно оставалось практически однородным; лишь звуковые волны, бегущие в разных направлениях, слабо возмущали его плотность.
До сих пор астрономы не знают точно, как произошло деление почти однородного вещества на звезды, но каким-то образом это случилось: когда возраст Вселенной еще не достиг 1 млрд лет, почти все ее барионное вещество оказалось поделено на плотные газовые шары-звезды с характерной массой 1030 кг, объединенные в галактики с массами порядка 1041 кг. Принципиальных трудностей в понимании этого процесса нет [2, 3]. Распространение звуковых волн создает в космическом веществе перепады плотности. В обычной звуковой волне в пределах комнаты сила упругости газа значительно выше силы гравитационного взаимодействия его частиц, поэтому в земных условиях гравитация не мешает циклическому колебанию звуковых волн. Но в космических масштабах эта картина может измениться: если в некоторых областях повышенной плотности газа его давление не способно противостоять его же собственному тяготению, то случайно возникшее уплотнение продолжит сжиматься. По-видимому, именно такой процесс гравитационной неустойчивости породил звезды и звездные системы [4], “власть” в которых окончательно “захватила” гравитация.
Гравитация - слабая, но всемогущая
Итак, в мире звезд “царствует” гравитация. Остальные физические взаимодействия - электромагнитное, слабое, сильное ядерное - практически никакой роли в движении звезд и в эволюции звездных систем не играют. Сила гравитации определяется чрезвычайно простым законом, изложенным И.Ньютоном в “Началах натуральной философии” (1687) и описывающим взаимодействие двух материальных точек. Но он применим и к протяженным телам, поскольку каждое из них можно представить в виде совокупности точек. Закон Ньютона гласит: две материальные точки, обладающие массами M1 и M2, притягиваются друг к другу с одинаковой силой, равной произведению их масс, деленному на квадрат расстояния между ними и, разумеется, умноженному на некоторую константу G (от лат. gravitas - тяжесть), значение которой зависит от единиц измерения массы, силы и расстояния:
F = GM1M2 / R2.
В системе СИ ([M] - килограмм, [R] - метр, [F] - ньютон) значение G = (6.673±0.001)·10–11. Обратите внимание, как коротка запись числа G - всего четыре значащие цифры; другие физические константы содержат по 8-10, а порой и 12 цифр. Почему же именно значение G измерено с такой низкой точностью? А потому, что гравитация - слабая сила, менее других проявляющая себя в лабораторных экспериментах. Очень трудно определить притяжение двух тел с аккуратно измеренной массой. Если два огромных слона (M1 = M2 = 4 т) стоят в лаборатории, тесно прижавшись друг к другу (R = 1 м), их взаимное гравитационное притяжение составляет всего 0.1 г. А вот если бы один слон состоял только из протонов, а другой - только из электронов, они притягивались бы с силой 1030 т! К счастью, все слоны, планеты и звезды состоят практически из равного количества протонов и электронов, электрическое взаимодействие которых уравновешивается. Зато гравитационное взаимодействие всех частиц суммируется, поскольку в природе нет гравитационных зарядов разного знака. Поэтому крайне слабая сила всемирного тяготения, почти незаметная между лабораторными телами, доминирует в мире космических тел.
Великие теоремы притяжения
Закон гравитации прост для математика, но физик и астроном помнят, что реальные тела не точки, а протяженные объекты. Значит, производя расчеты, придется иметь дело с интегрированием, т.е. с вычислением суммы сил, действующих на пробное тело со стороны всех частей какой-либо звезды или планеты. В наше время такую задачу нельзя назвать сложной: компьютер решит ее за секунды. Но во времена Ньютона многократное суммирование было чрезвычайно трудоемкой операцией, которую приходилось выполнять пером на бумаге. Поэтому Ньютон не продвинулся бы далеко в исследовании Вселенной, если бы не две замечательные теоремы, которые он доказал.
Теорема 1. Сферическое тело постоянной плотности притягивает находящуюся снаружи материальную точку так, как будто вся масса тела сосредоточена в его центре.Эта изумительная теорема дала возможность небесным механикам, вычисляющим движение звезд, планет и космических аппаратов, свести большинство задач о взаимодействии космических тел к задаче о притяжении двух точек. Счастье в том, что большинство небесных тел можно уподобить последовательности вложенных друг в друга сфер постоянной плотности. Например, у почти шарообразной Земли плотность растет к центру; разбив ее на бесконечное количество сферических слоев, мы убеждаемся, что каждый из них притягивает внешнюю точку так, будто вся его масса сосредоточена в центре. Поэтому никакого суммирования сил не требуется: с высокой степенью точности Земля притягивает внешние тела как точка.Теорема 2. Если материальную точку поместить внутри однородной сферы (причем в любом месте, а не только в центре), то она не ощутит притяжения этой сферы, поскольку силы, действующие на нее со стороны всех элементарных частей сферы, в точности уравновесятся.Эта теорема очень помогла тем специалистам, которые изучают недра небесных тел: стало возможным решать задачи, мысленно поместив наблюдателя внутрь планеты и не заботясь о тех слоях вещества, которые находятся снаружи от него, поскольку их суммарное притяжение равно нулю.Таким образом, вне сферы вы чувствуете, будто вас притягивает точка, а внутри сферы вообще невесомость. Благодаря этому даже во времена Ньютона, при полном отсутствии вычислительной техники, удавалось чрезвычайно точно решать важнейшие задачи: о внутреннем строении планет, в частности Земли, и об их взаимном притяжении и движении в пространстве.
Ньютон решил и задачу о том, как движутся две материальные точки, например планета и ее спутник, взаимно притягивающие друг друга по закону гравитации: они обращаются по эллиптической орбите вокруг общего центра масс, лежащего в фокусах эллипсов.
Решение Ньютона, полученное в конце XVII в., подтвердило эмпирические законы движения планет, найденные И.Кеплером в начале того же века. Если сила взаимодействия изменяется обратно квадрату расстояния, то спутник действительно должен двигаться по эллипсу, что и обнаружил Кеплер. Но теория Ньютона не только объяснила уже известные закономерности - она открыла и перспективу: эллипс оказался лишь частным случаем траектории; в зависимости от начальной скорости спутника ею могло быть любое коническое сечение - окружность, парабола, гипербола или, в предельном случае, прямая (рис. 1). В полной мере это многообразие возможных траекторий раскрылось в космическую эру.
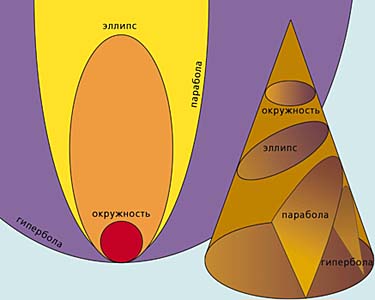
Рис. 1. Траектории движения в задаче двух тел.
Все возможные траектории представляются сечениями конуса плоскостью.Гравитация иных миров
Любопытно, что закон тяготения в формулировке Ньютона справедлив только в нашем, трехмерном пространстве. Если бы мы жили в геометрическом пространстве большего или меньшего числа измерений, закон притяжения имел бы иную форму. Легко понять, какую: если напряженность физического поля, связанного с обменом стабильными частицами (фотонами, гравитонами и т.п.), проинтегрировать по поверхности, окружающей источник этого поля, то должна получиться константа - полный поток частиц. Значит, если бы мы жили в эвклидовом пространстве N измерений, то закон Ньютона приобрел бы вид:
F µ 1 / RN–1
например в четырехмерном пространстве сила была бы обратно пропорциональна кубу расстояния.
К чему бы это привело? Будем менять показатель степени при R и посмотрим, как при этом станет двигаться пробное тело. На рис.2 показаны варианты такого движения для целого n = N–1, а на рис.3 - для нецелого n в законе
F µ 1 / RN
Среди наших примеров только для ньютоновского притяжения (n = 2) получилась простая замкнутая траектория - эллипс. Известно еще одно значение n, дающее эллиптическую траекторию: это n = –1, так называемый закон Гука, по которому меняется натяжение упругой нити. Но в этом случае центр притяжения лежит не в фокусе, а в центре эллипса.
Реальное движение планет
Зачем мы “издевались” над простым и изящным законом Ньютона, дающим зависимость 1/R2? Дело в том, что, обращаясь к реальным небесным объектам, мы замечаем их отличие от идеальных сфер. Форма Земли или Солнца лишь в первом приближении похожа на сферу. Известно, что Земля по причине вращения сплюснута вдоль полярной оси: расстояние между ее северным и южным полюсами на 43 км меньше, чем между противолежащими точками экватора. Из-за этого, к сожалению, теорема Ньютона в точности не выполняется, и Земля притягивает к себе не как помещенная в ее центре массивная точка - а по более сложному закону. Приблизительно его можно записать в форме, подобной ньютоновской:
F µ 1 / R2+d
где d<<1 - маленькая добавочка (которая, вообще говоря, может зависеть от R), положительная или отрицательная в зависимости от формы тела. Нарушается простота ньютоновского закона, а значит, нарушается и простота взаимного движения тел. При этом их орбиты, как мы видели, получаются незамкнутыми и гораздо более сложными, чем эллиптические.
Действительно, наблюдая за планетами, астрономы обнаружили, что все они движутся не точно по эллипсам, а скорее по “розеткам”. Разумеется, это никого не удивило, поскольку, начиная с Ньютона, все ясно понимали, что простой эллипс, как и сама задача о двух точках, лишь первое приближение к реальности. Учитывая взаимное притяжение планет, обращающихся вокруг Солнца, удалось почти полностью объяснить форму их орбит. Траектории спутников, близких к своим планетам, в основном искажаются из-за несферичности планет, а на движение далеких спутников (в их числе - Луна) решающее влияние оказывает Солнце.

Рис. 3. Траектории частицы при n немного меньшем (слева) или большем, чем 2.
Орбита, близкая к эллиптической, все время поворачивается.Используя законы Ньютона, астрономы XVIII-XIX вв. достигли высочайшего искусства в вычислении ожидаемых траекторий планет. Если наблюдаемое движение планеты отклонялось от расчетного, причину искали не в основах теории, а на небе - среди еще не открытых космических тел. Триумфом здесь стало теоретическое открытие планеты Нептун, которую “на кончике пера” обнаружили, разыскивая виновника возмущений в движении Урана, француз У.Леверье и англичанин Дж.Адамс в 1846 г.
Однако уже в XIX в. идиллии пришел конец: когда точность астрономических расчетов возросла, выяснилось, что теория Ньютона все-таки не стыкуется с наблюдениями. По иронии судьбы заметил это недавний триумфатор - Леверье, решивший после открытия Нептуна построить наиточнейшую теорию движения всех планет. Такую теорию он действительно построил, т.е. разработал аналитическую схему вычисления положения планет; однако не все в этой схеме получило физическое объяснение.
Например, ближайшая к Солнцу планета Меркурий движется по довольно вытянутой эллиптической орбите, поворот оси которой легко заметить. Обычно этот поворот выражают как скорость углового перемещения перигелия - ближайшей к Солнцу точки орбиты. Наблюдения показывают, что перигелий Меркурия поворачивается на 574'' за столетие в сторону движения самой планеты. Леверье доказал, что поворот на 531'' за 100 лет вызван влиянием других планет - в основном Венеры, Юпитера и Земли. Это 93% от наблюдаемого эффекта; казалось бы, можно радоваться. Но оставшиеся 43'' в столетие не давали астрономам покоя: сказывалась профессиональная гордость за пресловутую астрономическую точность [5, 6].
Обнаружив неувязку в движении Меркурия, Леверье решил, что ему вторично улыбнулась удача, как в случае с Нептуном. Он вычислил параметры неизвестной планеты, которая могла бы находиться внутри орбиты Меркурия и дополнительно возмущать его движение. Этой гипотетической планете даже придумали имя - Вулкан. Ее долго искали, но не нашли. Поэтому к концу XIX в. в небесной механике возник парадокс: ньютоновская физика объясняет движение всех тел Солнечной системы, кроме Меркурия.
Чтобы спасти физику, было предложено множество оригинальных гипотез; самые горячие головы даже покушались на святое - на закон гравитации Ньютона, предлагая его немного модернизировать. Действительно, движение Меркурия удавалось объяснить, если принять n = 2.00000016. Но чувство прекрасного не позволяло физикам без отвращения смотреть на закон гравитации в такой форме:
F = GM1M2 / R2.00000016.
К счастью, пришел Эйнштейн и объяснил, что теория Ньютона - это лишь первое (хотя и очень хорошее!) приближение к описанию природы, на самом же деле движение тел и их гравитационное взаимодействие устроены сложнее.
Теория Эйнштейна и сплюснутость Солнца
Вместо мелких поправок к ньютоновской теории тяготения Эйнштейн внес в физику нечто совершенно новое - общую теорию относительности (ОТО). Правда, ее математическая форма не так проста, как у ньютоновской теории, зато она правильно описывает притяжение и движение тел. Когда на основе ОТО было рассчитано движение Меркурия, в частности поворот его эллиптической орбиты, теория сошлась с наблюдениями в пределах такой точности, какую только могут дать современные астрономы. Даже значительно меньший эффект - поворот эллиптической орбиты Земли всего на 4'' в столетие - весьма точно объясняется в рамках ОТО [7].
Но спустя время в замечательном согласии эйнштейновской физики с астрономическими наблюдениями был также усмотрен парадокс. Суть его в том, что все расчеты, как по Ньютону, так и по Эйнштейну, проводились для сферического Солнца, будто вся его масса сосредоточена в центре. Но Солнце вращается, значит, сферическим оно быть не может. В телескоп мы наблюдаем вращение его поверхности с периодом 25.4 сут.
Если с таким же периодом вращаются и недра Солнца, то фигура его должна быть сплюснутой с относительной разностью экваториального и полярного радиусов Dr/r ~ 10–5. Если же внутренность Солнца вращается иначе, то и сплюснутость будет иная.
В 1960-е годы американский физик Р.Дикке, один из создателей конкурирующей с ОТО релятивистской теории (скалярно-тензорная теория Бранса-Дикке), обратил внимание на то, что формулы Эйнштейна используются для расчета движения планет вокруг сферического Солнца. Но раз Солнце вращается и не может быть шаром, значит, нужно принять это во внимание и пересчитать все заново, решил Дикке. В то время технические трудности релятивистских расчетов для неточечных масс уже были преодолимы - появились компьютеры. Но требовалось точно знать, какова форма Солнца и как именно оно вращается. Теория Эйнштейна утверждает, что на силе притяжения объекта сказывается не только отличие его формы от идеального шара, но и характер вращения: даже тяготение идеального шара будет разным в зависимости от того, неподвижен он или вращается. Гравитационное поле вращающегося тела в рамках ОТО имеет вихревой компонент: тело не только притягивает соседние объекты, но и раскручивает их вокруг себя.
В 1969 г. Дикке на основе своих измерений определил сплюснутость Солнца Dr/r = 5·10–5. Для медленно вращающегося Солнца это слишком много; но Дикке указал, что недра Солнца могут вращаться значительно быстрее поверхности. Если основная масса нашей звезды совершает оборот менее чем за 2 сут, то центробежная сила деформирует ее именно так, как показали измерения [8]. В окрестности сплющенного Солнца закон притяжения, как мы знаем, отличается от 1/R2, причем не только в эйнштейновской, но и в ньютоновской теории. Если учесть классический вклад солнечной фигуры в движение перигелия Меркурия, то остающаяся релятивистская поправка уже не совпадает в точности с предсказанием ОТО, а скорее подтверждает (как вы уже, наверное, догадались) теорию гравитации Бранса-Дикке.
Правда, измерения других исследователей не подтвердили сильную сплюснутость Солнца. До конца эта проблема не решена по сей день. Уже многие годы над ней работают астрономы и физики: одни изучают Солнце, измеряют скорость его вращения и степень сплюснутости, другие рассчитывают движение планет вокруг вращающейся и сжатой звезды в рамках различных теорий тяготения.
Жидкие тела вращения
Итак, гравитационное поле звезды зависит от ее формы и скорости вращения. Но и сама форма зависит от вращения. Посмотрим, как связаны эти параметры. На рис.4 показана последовательность фигур равновесия самогравитирующих тел. Странным словом “самогравитирующее” обозначают тот факт, что тело подвержено только действию собственной силы тяжести, которой противостоит внутреннее изотропное давление. Рисунок построен в координатах “квадрат безразмерного углового момента j - квадрат безразмерной угловой скорости w”:
j = Jr1/6 / 2M5/3ЦpG, w = W / Ц4pGr
где M, r, J, W - масса, плотность, момент импульса и угловая скорость вращения тела соответственно. Линии на рисунке показывают решения уравнений равновесия, т.е. указывают, с какой угловой скоростью будет вращаться тело, обладающее определенным моментом импульса. Темными линиями указаны решения для тел из несжимаемой жидкости. Почему взяты жидкие? Это удобная абстракция: идеальная жидкость под давлением не меняет свою плотность, но при изменении вращения меняет форму - поверхность жидкости всегда перпендикулярна сумме всех действующих на нее сил, включая центробежные. Некоторые космические тела, например планеты, действительно можно считать жидкими, поскольку их плотность слабо меняется с глубиной. Но для звезд эта абстракция не подходит: плотность их вещества сильно меняется от центра к поверхности. Поэтому для них рассчитана последовательность фигур сжимаемых тел (фигуры Джинса).
Может показаться, что в приложении к космическим телам наше исследование лишено смысла: где это видано, чтобы кто-то раскручивал планету или звезду. Заметим, что иногда бывают ситуации, когда взаимодействие двух близких тел (например, планеты и ее спутника) приводит к существенному изменению их момента импульса. Но чаще тела действительно сохраняют момент, однако заметно меняют плотность. Например, в ходе формирования звезды из разреженного облака ее размер уменьшается почти в 106 раз, а плотность возрастает в ~ 1017 раз! Математически это эквивалентно росту j.
Продолжим наш мысленный эксперимент, глядя на рис. 4. От последовательности фигур Маклорена в двух точках бифуркации отходят новые кривые. Это также последовательности фигур равновесия, которые были открыты позже, чем сфероид Маклорена. Если сообщим телу момент импульса чуть больший, чем у первой точки бифуркации, и немного возмутим его форму, оно может скачком превратиться из “тыквообразного” сфероида Маклорена в “дынеобразный” эллипсоид Якоби, т.е. станет не сплюснутым, а вытянутым, и будет устойчиво вращаться вокруг оси, перпендикулярной направлению вытянутости. Если раскручивать еще сильнее, тело будет становиться все более вытянутым, пока не превратится в спицу.
Вторая точка бифуркации на кривой Маклорена связана с превращением диска в кольцо. При определенном моменте выше критического диск становится неустойчивым: за счет центробежных сил вещество из его серединки может вдруг отскочить к периферии, и получится кольцо. Казалось бы, это математическая экзотика, но недавно в областях формирования звезд были обнаружены именно такие объекты [9].
На линии Якоби также видна точка бифуркации. У сильно вытянутого эллипсоида при моменте импульса больше критического вещество может из центра отойти к краям, создав в середине перемычку. Получается фигура, похожая на земляной орех, - гантель Пуанкаре.
Почти каждая из представленных здесь фигур носит имя известного математика или физика. Вот так “просто” можно прославить свое имя в науке - достаточно найти новую фигуру равновесия вращающегося тела. И многим это удалось: на рисунке представлены далеко не все возможные формы вращающихся жидких тел. Некоторые из них весьма сложны, и любая может быть присуща планете или звезде. А это значит, что их соседи-спутники будут взаимодействовать не с материальной точкой, а, например, с бешено вращающейся гантелью. Интереснейшая задача - исследовать движение спутника такой гантели!
Приливы в звездах
От формы звезды зависит взаимодействие с соседями, а те в свою очередь влияют на ее форму. Рассмотрим близкий пролет двух случайных звезд (рис. 5). Если в процессе сближения они остаются шарообразными, то притягиваются по закону Ньютона, а значит, движутся по гиперболическим траекториям и после сближения вновь расходятся “на бесконечность”. На самом же деле взаимное приливное влияние искажает форму звезд - они становятся вытянутыми эллипсоидами, и это влияет на их движение.
Приближаясь друг к другу, звезды вытягиваются вдоль соединяющей их прямой. Этот эффект называют приливным по аналогии с морскими приливами, возникающими на Земле под влиянием Луны. Как и в земных океанах, на поверхности звезды возникают приливные выступы - горбы, а поскольку звезды движутся, приливный горб пытается отследить направление между ними. Но в силу инерции и вязкости он не может точно следовать движению звезд: сначала запаздывает, а затем опережает его. В результате взаимодействие происходит не по ньютонову закону: более близкий горб притягивается сильнее, чем более далекий, а следовательно, возникает составляющая силы притяжения, тормозящая движение звезды по орбите и уводящая ее с простой гиперболической траектории. Звезда переходит на эллиптическую орбиту и оказывается навсегда привязанной к тому светилу, с которым она случайно сблизилась. Так из двух одиночных звезд образуется двойная система.

Рис.5. Близкий пролет двух звезд без учета (слева) и с учетом приливного эффекта.
Для простоты одна из звезд (черная) изображена неподвижной и
абсолютно жесткой, недеформируемой.Формирование двойных систем влияет на эволюцию звездного скопления, в котором они живут [10]. Объединившись, звезды весьма своеобразно взаимодействуют друг с другом и с одиночными членами скопления, заставляя последних двигаться более интенсивно. От встреч с другими звездами быстро эволюционируют и сами двойные светила. Некоторые из них сближаются и обмениваются веществом, что приводит к их “омоложению” и порождает весьма экзотические объекты, обнаруженные за последние годы в звездных скоплениях - рентгеновские и ультрафиолетовые источники, вспыхивающие звезды и быстрые пульсары, молодые белые карлики и “омолодившиеся” нейтронные звезды. А в основе этого астрофизического разнообразия лежит гравитационное взаимодействие звезд, в котором еще немало загадок.
Литература
1. Смольников А.А. Темная материя во Вселенной // Природа. 2001. №7. С.10-19.
2. Силк Дж. Большой взрыв: рождение и эволюция Вселенной. М., 1982.
3. Сурдин В.Г., Ламзин С.А. Протозвезды. М., 1992.
4. Джинс Дж. Движение миров. М., 1933.
5. Бергман П. Загадка гравитации. М., 1969.
6. Роузвер Н.Т. Перигелий Меркурия: от Леверье до Эйнштейна. М., 1985.
7. Боулер М. Гравитация и относительность. М., 1979.
8. Дикке Р. Гравитация и космология. М., 1972.
9. Сурдин В.Г. Рождение звезд. М., 2001.
10. Сурдин В.Г. Судьба звездных скоплений // Природа. 2001. №4. С.44-50.