А.Шкроб: НАУКА ЧЕРНОГО ЯЩИКА

Уже с первых шагов компьютерной техники люди с тревогой и нетерпением ожидали, когда вычислительные процедуры в машинах станут реально конкурировать с человеческим разумом. Эта тема вот уже более полувека не дает покоя не только фантастам и футурологам, но и ученым, пытающимся понять специфику человеческого интеллекта и предугадать его функции и роль в цивилизации, опирающейся на компьютерные технологии получения и обработки информации.

Мы инстинктивно боимся перспективы вытеснения человеческого мышления из тех сфер деятельности, которые принято называть творческими: искусства, литературы и науки, особенно науки. Опасения, что большинство людей утратит точки приложения природных дарований, сочетаются при этом со страхом перед интеллектом, свободным от чисто человеческих свойств: совести, стыда, любви…

На этом фоне часто ускользают от внимания реальные процессы столь глубокого проникновения компьютерных технологий в науку, что оно не только ускоряет исследования и повышает их результативность, но кардинально изменяет характер деятельности и мышления ученых.

До настоящего времени подобные революции в научной методологии были связаны с грандиозными идеями. Дифференциальное и интегральное исчисления, дарвиновская теория естественного отбора, статистическая механика, квантовая и релятивистская физика, открытие информационной роли ДНК - все это не просто вехи развития естествознания, но события, изменившие самую ткань науки и определившие формы и стиль ее развития. Характерно, что все эти великие свершения были плодами наблюдений или размышлений и лишь в относительно малой степени зависели от уровня развития технологии.

Да, бурное развитие науки в XIX и особенно в ХХ веке было бы немыслимо без оптических и электронных микроскопов, ускорителей частиц и другого хитроумного и могучего инструментария. Именно инструментария! - потому что все эти штуки были лишь продолжением рук исследователя, и вовсе не посягали на участие в его аналитических функциях.

Сегодня же мы становимся свидетелями рождения новых форм научной деятельности, в которых технические устройства - компьютеры - компенсируют не слабость человеческих органов чувств или ограниченность физических сил, но недостаточность нашего разума. И дело здесь далеко не всегда сводится к неспособности исследователя быстро произвести в уме или на бумаге необходимые вычисления.

Я попытаюсь изложить суть проблемы на примерах из близких мне направлений биохимии. Это не случайный выбор, поскольку интересующая нас тенденция проявляется, прежде всего, при изучении наиболее сложных объектов, в частности, живой материи. Некогда Шредингер определил ее устройство как "апериодический кристалл", имея в виду, что высочайшая степень упорядоченности соединяется в ней с предельной неоднородностью. Но сначала - немного о том, как вообще наука постигает окружающий нас мир и что означает это слово - "постигает".

* * *

Френсис Бэкон, чтимый как отец научной методологии, едва ли не главным своим достижением считал учение о так называемых инстанциях. На современном языке оно сводится к созданию абстрактного описания изучаемого объекта путем отбрасывания тех его свойств, которые несущественны для решаемой проблемы. Так, например, будет ли шататься на плоском полу стол, зависит не от цвета покрывающего его лака или стиля декоративных элементов, а от его тяжести, числа, длины и жесткости ножек.

Такого рода абстракции принято называть моделями, и они составляют суть научных представлений и главное орудие обобщений. Общим свойством моделей является то, что они значительно проще реальных прототипов, а вот степень допустимых упрощений… Очень часто она определяется возможностью описания (не обязательно математического), позволяющего, в конечном итоге, делать количественные или качественные предсказания. Именно и только предсказательные возможности оправдывают сделанные упрощения. Так, например, в космонавтике в одних случаях Землю можно рассматривать как шар, а в других приходится учитывать ее истиную форму - геоид. Упрощения и ограничения, лежащие в основе классической физики, неприменимы при субсветовых скоростях и вблизи объектов гигантской массы. Мы говорим об адекватности модели, если сохраненные в ней черты реального объекта необходимы и достаточны, чтобы правильно предсказывать его поведение в заданном диапазоне условий.

В большинстве случаев модели, создаваемые нашим разумом, сознательно или бессознательно удовлетворяют еще одному, правда трудно формализуемому критерию - они должны быть "понятны". Иными словами, они согласуются с нашими знаниями и опытом, с интуицией, со всем тем, что объединяет понятие "здравый смысл". Моделям, противоречащим "здравому смыслу", наш разум сопротивляется - оттого так трудна для понимания квантовая теория, хотя она и обладает бесспорной предсказательной силой. Сами того не замечая, мы мыслим моделями, их структура, скорее всего, как-то связана с устройством и механизмами мозга, с отпечатком, наложенным на них обучением, - видимо, именно в этом причина такого рода конфликтов.

Иногда сложность объекта побуждает к созданию моделей, в рамках которых мы сознательно отказываемся от возможности проследить все причинно-следственные связи. Так, например, при описании газов рассматривается не каждая из молекул, а лишь их ансамбль. В итоге, предсказания для отдельной молекулы носят не точный, а лишь вероятностный, статистический характер. Сейчас, спустя полтора века после Максвелла и Больцмана, нам трудно представить, насколько нетривиальным и смелым был такой подход. Его оправданием было получение лаконичных уравнений, "понятных" лишь в том смысле, что мы можем мысленно анализировать вклады входящих в них параметров.

Увы, для очень сложных изучаемых объектов, утрачивается и такая форма "понятности" моделей. Например, поведение под нагрузкой сложных конструкций описывается такой большой и запутанной системой дифференциальных уравнений, что ее аналитическое решение невозможно, - иными словами, нельзя получить обычное уравнение и, пользуясь им, подобрать оптимальные размеры и свойства отдельных конструкционных элементов. Возможно лишь численное решение, то есть, по существу, математический эксперимент, при котором мы последовательно используем разнообразные сочетания параметров и получаем ответ для каждого конкретного случая. Разумеется, провести такой эксперимент дешевле и быстрее, чем строить и ломать реальные конструкции…, пока степень сложности не возрастает настолько, что перебор всех возможных значений параметров не упирается в ограниченность вычислительных мощностей.

Подытожим сказанное… В своем стремлении постичь окружающий мир, то есть научиться предсказывать свойства и поведение окружающих нас объектов (а заодно и самих себя!), наш разум создает их абстрактные модели - упрощения, позволяющие выделить и обобщить наиболее существенные черты реальности. Мерилом "понятности" этих моделей можно считать возможность для человека проследить в них причинно-следственные связи. Однако, с увеличением степени сложности объекта его адекватные модели сами становятся настолько сложными, что утрачивают свою "понятность". И тогда меняется акцент: модели вынужденно становятся не столько средством, сколько объектом изучения - симуляторами, более удобными для экспериментирования, чем реальные прототипы. При этом мы в той или иной мере отказываемся от "понимания", но сохраняем способность предсказывать.

* * *

Давайте проследим эту трансформацию роли моделей на примере изучения структуры и функции белков - важнейших компонентов живой материи. При невероятном разнообразии выполняемых задач (катализаторы, регуляторы, рецепторы, структурные элементы и т.д.) белки устроены химически довольно просто, являясь полипептидами - линейными полимерами всего 20-ти природных аминокислот. Весь фокус в том, каждый белок, а их в живой природе миллионы, отличается строго индивидуальным распределением аминокислотных остатков в пептидной цепи. Эта последовательность остатков - ее называют первичной структурой белка - однозначно определяет пространственное (иногда говорят - трехмерное) строение белковой молекулы, то есть то, каким манером полипептидная цепь сворачивается в некую объемную конструкцию - белковую глобулу. Именно особенности пространственных структур белков - сложных и разнообразных - позволяют этим биополимерам выполнять их жизненно важные функции.

За время жизни одного поколения люди научились и "читать" аминокислотные последовательности белков, и определять пространственную структуру их молекул. Эти экспериментальные процедуры непрерывно совершенствуются. Если лет тридцать-сорок назад установление первичной структуры белка было трудовым подвигом коллектива работников, то сейчас это рутинный эксперимент, доступный старшекурснику. Что там отдельный белок, когда один за другим определяются полные геномы целых организмов, а это автоматически приводит к каталогизации последовательностей всех присущих им белков.

К сожалению, по своей производительности экспериментальные методы определения пространственной структуры белков (дифракция рентгеновских лучей в белковых кристаллах, ядерный магнитный резонанс и др.) катастрофически отстают от "чтения" последовательностей. Не меньшая беда и в том, что для этого требуются вполне ощутимые количества самих белков, что по многим причинам, как правило, достаточно затруднительно. Между тем, знание пространственного строения белков абсолютно необходимо для чисто практических нужд, например, для создания искусственных вакцин и новых эффективных лекарственных веществ. Отсюда - насущная потребность выработки принципиально иных, чисто аналитических подходов, перебрасывающих мосты непосредственно от аминокислотной последовательности пептидной цепи к ее трехмерной упаковке.

Но и этого мало! Функционирование белков сопряжено с локальными флуктуациями их структуры, вызванными незначительными согласованными поворотами атомов вокруг связей между ними. Такие флуктуации называются конформационными изменениями, и они, в частности, являются важнейшим элементом ферментативного катализа, рецепции внешних сигналов, взамодействия с различными биорегуляторами. Это означает, что для понимания механизма действия белков и сознательного воздействия на них важно представлять себе не только статическое состояние белковых молекул, но также и их динамику. По этому поводу известный венгерский биохимик Ф. Штрауб некогда мрачно пошутил: "Мы можем подвергнуть Джоконду рентгеноскопии и выяснить, как расположены в ней все атомы, но при этом не узнаем, кому и зачем она улыбается". Увы, разрыв между экспериментальными методами определения трехмерной структуры белков и регистрации их молекулярной динамики куда больше, чем между получением дагерротипа и современной сверхскоростной киносъемкой…

Решения обеих проблем были найдены с помощью моделей молекул белка. Начало этому было положено еще в годы войны советскими учеными С.Е. Бреслером и Д.Л. Талмудом. В 1944 году они предложили так называемую капельную модель строения водорастворимых белков, которая сохранила свое значение и поныне. Как известно, аминокислотные остатки в белках по свойствам боковых цепей делятся на полярные и неполярные (иначе их зовут гидрофобными). Полярные остатки "предпочитают" находиться в контакте с молекулами воды, тогда как неполярные этого "избегают". Согласно капельной модели, полипептидная цепь белка сворачивается таким образом, чтобы удовлетворить эти требования, так что внутренние области белковой глобулы напоминают жировую каплю, отделенную от водной среды прослойкой полярных остатков. Несмотря на кажущуюся примитивность, эта модель совершенно правильно отражает реальную картину, однако неспособна предсказать, как именно упакована в глобуле полипептидная цепь.

Чтобы определить это, обращаются к своего рода "механическим" моделям белка, при построении которых в вычислительных алгоритмах имитируются силы взаимодействия между атомами и упругие свойства межатомных связей. Такого рода модели неплохо показали себя в случае коротких пептидных молекул. Так, в 70-х годах Е.М. Попов в Институте биоорганической химии расчетным путем установил строение депсипептидного антибиотика валиномицина. Он был озадачен тем, что полученная структура отличается от предложенной ранее его коллегами по институту Ю.А. Овчинниковым и В.Т. Ивановым, но оказалось, что она полностью соответствует неоспоримым данным рентгеноструктурного анализа, выполненного американскими исследователями.

К сожалению, использование подобного подхода к определению пространственной структуры белков встречает колоссальные трудности. Во-первых, при этом требуются пока практически недостижимые вычислительные мощности. Во-вторых, среди необъятного множества допустимых структур на каждом этапе вычислений можно выделить группу предпочтительных, но среди них крайне трудно выбрать ту единственную, которая присутствует в природном белке. В-третьих,… В-четвертых… Коротко говоря, применительно к белкам, этот метод пока не нашел сколько-нибудь широкого применения.

И вот тут пора вернуться к нашей основной теме… Как поступить, если необходимо предсказать свойства некоторой системы при том, что неизвестны законы, определяющие зависимость между параметрами, которые описывают состояние этой системы. В этом случае традиционно используют так называемые корреляционные методы. Суть этих методов состоит в том, что имеющиеся опытные данные используются для построения не имеющих физического смысла зависимостей, которые мало отличаются от истинных. Так, например, точки лежащие на коротком участке гиперболы можно вполне удовлетворительно аппроксимировать полиномом. Представьте, что вам неизвестен гиперболический характер истинной кривой, - тем не менее, пользуясь полиномом, можно с достаточной точностью вычислять положение любой точки в заданном интервале. Правда, мы так и не узнаем, что имели дело с гиперболой…

Нечто подобное сейчас широко используют для компьютерного предсказания трехмерной структуры белков. К настоящему времени уже известны структуры сотен белков, и можно оценить вероятность, с которой данный аминокислотный остаток в данном окружении находится в составе того или иного типового конструкционного элемента белковых молекул, скажем, a-спирали или складчатого листка. Можно также найти в известных белках фрагменты, сходные по последовательности с фрагментом неизвестного белка, и приписать последнему аналогичную структуру. И так далее… Удивительно, но пользуясь подобными аналогиями, часто удается угадать истинную структуру неизвестного белка. Уже одно это показывает единство законов укладки полипептидных цепей в белках, хотя ничуть не приближает к их пониманию.

ДУРНОЙ ПРИМЕР ЗАРАЗИТЕЛЕН

Еще недавно большинство биохимиков было убеждено, что пространственная структура белков в живых клетках (ее называют нативной) однозначно и всегда определяется их аминокислотными последовательностями. И в самом деле, белок можно синтезировать или полностью развернуть его глобулу разными хитрыми способами, но обычно удается подобрать условия, при которых он свернется в нативную структуру. Наконец, гены одного организма можно экспрессировать в другом, получая при этом нативные белки.

Представляете, как трудно пришлось бы клеткам, если бы полипептидная цепь белка могла упаковываться по-разному, и эти формы были способны переходить одна в другую? Нет, нет - никогда!, - это неимоверно усложнило бы всю регуляцию клеточного хозяйства. Более того, мы можем только удивляться мудрости Природы, предельно усложнившей такого рода переходы. Как? Это - хороший вопрос, но ответ довольно сложен… Вкратце, глобальные конформационные изменения белков на своем пути требуют синхронного разрыва многих водородных связей, погружения полярных остатков в неполярное окружение и, напротив, обнажения гидрофобных остатков для молекул воды.

И, тем не менее, оказалось, что немыслимое - возможно. Все началось с попыток выделить возбудители странных, неизлечимых и очень медленно развивающихся заболеваний человека и животных, которые вызывают специфическую дегенерацию мозга. Поначалу никто этому не верил, но оказалось, что их возбудителями являются не бактерии или вирусы, а… сравнительно небольшие белки (их назвали прионами от английского proteinaceous infection - белковая инфекция). Эти белки существуют в двух конформациях: нормальной (a) и патогенной, прионовой (b) (см. рисунок). Нормальные белки - естественные компоненты клетки, которые никогда не переходят в прионовую форму. Однако, если они, не дай бог, встретятся с прионом, то превращаются в прионы. В результате возникают агрегаты прионового белка - так называемые амилоидные бляшки, - которые и являются причиной заболевания. В целом процесс носит автокаталитический характер, поскольку вновь образующиеся прионы сами провоцируют конформационные превращения "здоровых" молекул.

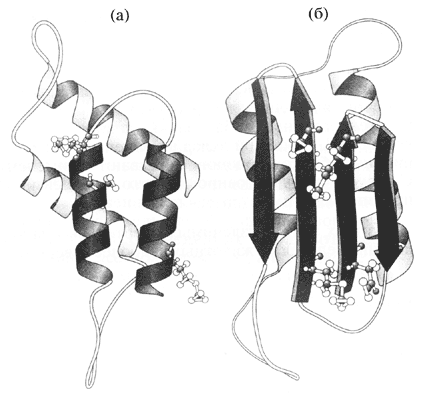
Предполагаемое изменение укладки полипептидной цепи
при превращении нормального белка (а) в прион (б).
Завитками показаны a-спирали, а стрелами - компоненты складчатого листка

Невероятно, но факт, к тому же удостоверенный Нобелевской премией, которую несколько лет назад получил Стенли Прузинер - отец прионов. Более того, сейчас есть основания полагать, что сходные явления имеют место не только в патологии, но также и при постоянно протекающих перестройках так называемого цитоскелета - важнейшего структурного элемента эукариотических клеток. И, тем не менее, это все же скорее исключение, экзотика… Подавляющее большинство белков имеет единственную нативную конформацию, которая в норме способна лишь к незначительным изменениям.

Коль скоро трехмерная структура белка так или иначе определена, ее можно использовать для создания математической модели - компьютерного отображения, которое воспроизводит геометрию молекулы, а, при необходимости, ее механические и прочие свойства. Такая модель бесценна в качестве симулятора реального белка при решении многих научных и прикладных задач.

Рассмотрим, например, создание новых лекарственных препаратов, которые обычно являются ингибиторами или активаторами ферментов, то есть белков, катализирующих те или иные биохимические процессы. Любой регулятор активности фермента должен для своего действия связаться с этим ферментом, а для этого поверхности молекул регулятора и фермента в области контакта обязаны быть взаимно дополнительны (это называют комплементарностью). Мы можем выделить на математической модели желаемый участок связывания и далее либо искать среди великого множества уже известных органических соединений те, молекулы которых комплементарны этому участку, либо сконструировать такое соединение заново. Напомню, что речь идет о вычислительном эксперименте, который осуществляется значительно быстрее и стоит много дешевле как реального тестирования, так и реального синтеза. Разумеется, они понадобятся, но уже не будут носить массовый характер.

Однако не все так просто… Связывание белков друг с другом или с низкомолекулярными биологически-активными соединениями, взаимодействие ферментов с их мишенями - субстратами - все эти процессы, как уже упоминалось выше, сопровождаются конформационными изменениями белковых молекул. Эти изменения обычно невелики, но могут захватывать значительную область белка. Именно так информация о связывании и энергия, выделяющаяся при связывании, могут передаваться с одного конца белковой молекулы на другой. "Механические" модели позволяют имитировать эти эффекты, и мы можем с их помощью констатировать, что, скажем, связывание такого-то регулятора снижает сродство фермента к субстрату. Однако, в силу малости и размазанности конформационных изменений, далеко не всегда удается их проследить и, таким образом, механизм этого явления остается "непонятным".

Это не редкий и частный случай. Сходная проблема возникает, например, когда нужно проследить, как замены отдельных аминокислотных остатков сказываются на неких свойствах белка, например, когда требуется увеличить теплоустойчивость ферментов, примешиваемых к стиральным порошкам для разрушения белковых и жировых загрязнений. Иногда речь идет не столько о самих конформационных изменениях, сколько о воздействии на жесткость структуры, влияющей на характер и амплитуду потенциальных конформационных изменений. Так или иначе, мы опять встречаемся с ситуацией, когда модель позволяет делать предсказания, не проясняя сути происходящего.

* * *

Головокружительные успехи геномики и протеомики приближают время, когда нам станут известны структуры и функции буквально всех белков. И это будет время рождения новой биологии, поскольку откроется возможность изучения всей совокупности явлений, когда параллельно, а когда последовательно протекающих в отдельных клетках и целых организмах. Именно эти динамические процессы составляют суть Жизни, ибо вне их мы имеем дело не живым существом, а с его свежим трупом.

Каждый студент-биохимик цепенеет от ужаса при первом знакомстве с так называемыми метаболическими картами, на которых изображены известные биохимические реакции. Зрелище действительно впечатляющее, однако при всей сложности и запутанности схемы метаболических реакций - детская игра по сравнению со схемами их регуляции. Для этого предусмотрены многоэтажные и взаимосвязанные иерархически организованные методы контроля, пространственное и временное разделение процессов, бесчисленные приспособления для прямых и обратных связей и т.д. Ясно, что впереди нас ожидает только усложнение представлений о динамике жизненных процессов.

Между тем, данные о биохимической динамике имеют далеко не только академический интерес. Они являются базой для анализа и предсказания возможных последствий любых воздействий на организм, будь то генноинженерное вмешательство, химиотерапия, инфекция и т.д. Анализом скоростей химических реакций занимается наука, именуемая кинетикой - одна из ветвей физической химии, главным оружием которой служит описание процессов дифференциальными уравнениями. Можно смело утверждать, что кинетика и близко не подходила к описанию столь сложных явлений как совокупность внутриклеточных реакций. Но заняться этим ей придется, и тогда, в лучшем случае, повторится описанное выше. Математические модели можно будет использовать в качестве удобных для экспериментирования симуляторов реальности, но проследить в них причинно-следственные связи будет крайне сложно.

* * *

Итак, на примере некоторых биологических проблем мы попытались показать, как сложность изучаемых объектов сказывается на методологии научных исследований и мышлении исследователя. Общая тенденция, повидимому, состоит в том, что модели реальности, ранее служившие только средством обобщения и "прояснения" окружающего нас мира, все более превращаются в способ его симуляции. Виртуальный мир симуляций, разумеется, проще реального, но не настолько, чтобы стать полностью "понятным". Тем не менее, мы используем компьютерные симуляции вместо реальных объектов просто потому, что при удачном выборе алгоритмов, вычислительных программ и "железа", достаточно велик шанс получить правильные предсказания. Такой подход бессмыслен для относительно простых изучаемых объектов, при некотором уровне сложности он вступает в конкуренцию с традиционным, а для очень сложных объектов - ему пока нет альтернативы.